We discussed the above equation in class. Gradient theorem is used to show
However, gradient theorem applies in converting volume integration to surface integration not surface integration to line integration. For that purpose, we have the Green's theorem, which states
Sorry about the equation not showing up. Green's theorem applies to general curve on 2D surface not just rectangular ones. In general we have
You can set M=0 or L=0 to obtain
In these equation, we have dx=n_x*ds and dy=n_y*ds. These equations are valid for any arbitary curve in 2D surface. Gradient theorem doesn't apply in this 2D case.
Haodong, thanks a lot for the question. However, the Green's theorem you mentioned can be shown to be the same as the the gradient theorem if you are careful enough. I will leave it as a challenge for your guys first. Then I will provide the answer. Hint, Green's theorem using dx and dy, we used ds. dx and dy are related to ds. Green's theory, the curve must be positively oriented.
Oh, that's a stupid mistake I ever made... But it still feels a little bit confusing why gradient theorem applies in 2D case. Maybe we should consider gradient theorem as a more fundamental theorem than Divergence theorem or Stokes theorem because it has the same form for 1D-2D and 2D-3D case. It seems like it could be extended to even higher dimensions as well
I didn't read about this topic carefully enough. It always feels hard to memorize all those tensor calculus equations and I refer to textbook a lot, which is not actually necessary if you think of it in a unified form. For others who might be interested, I recommend you read through the wikipedia about stokes theorem and divergence theorem.
Haodong Du @ on
We discussed the above equation in class. Gradient theorem is used to show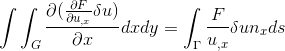
However, gradient theorem applies in converting volume integration to surface integration not surface integration to line integration. For that purpose, we have the Green's theorem, which states
Therefore, we should have
Report abuse
Haodong Du @ on
Sorry about the equation not showing up. Green's theorem applies to general curve on 2D surface not just rectangular ones. In general we have
You can set M=0 or L=0 to obtain
In these equation, we have dx=n_x*ds and dy=n_y*ds. These equations are valid for any arbitary curve in 2D surface. Gradient theorem doesn't apply in this 2D case.
Report abuse
Wenbin Yu @ on
Haodong, thanks a lot for the question. However, the Green's theorem you mentioned can be shown to be the same as the the gradient theorem if you are careful enough. I will leave it as a challenge for your guys first. Then I will provide the answer. Hint, Green's theorem using dx and dy, we used ds. dx and dy are related to ds. Green's theory, the curve must be positively oriented.
Report abuse
Haodong Du @ on — Edited @ @ on
Oh, that's a stupid mistake I ever made... But it still feels a little bit confusing why gradient theorem applies in 2D case. Maybe we should consider gradient theorem as a more fundamental theorem than Divergence theorem or Stokes theorem because it has the same form for 1D-2D and 2D-3D case. It seems like it could be extended to even higher dimensions as well
Report abuse
Haodong Du @ on
I didn't read about this topic carefully enough. It always feels hard to memorize all those tensor calculus equations and I refer to textbook a lot, which is not actually necessary if you think of it in a unified form. For others who might be interested, I recommend you read through the wikipedia about stokes theorem and divergence theorem.
Report abuse