Viscoelastic Beam Properties of a TRAC Boom
In this example, we want to compute the Viscoelastic effective properties of a TRAC Boom fabricated from plain woven composite material made of isotropic viscoelastic matrix and transversely isotropic elastic fiber. The fiber properties are defined by means of engineering constants as specified in the table below.
(Image(Fiber_properties.png, desc="Fiber properties defined as transversely isotropic elastic") failed - File not found)
The matrix properties are given by means of the Prony coefficients presented in the table below and we will consider that the matrix has a constant Poisson’s ratio equal to 0.33.
(Image(Resin_properties.png, desc="Prony coefficients and relaxation times for the matrix") failed - File not found)
We will use a square pack 2D SG with fiber volume fraction equal to vf = 0.64.
Software Used
We will use TexGen4SC, SwiftComp 2.1 and Abaqus CAE with the Abaqus SwiftComp GUI for this tutorial. TexGen4SC will be used to run the viscoelastic homogenization of the fiber-matrix square pack microstructure and also for the viscoelastic homogenization of the plain weave laminate. Abaqus CAE will be used to model the TRAC boom and to run the viscoelastic homogenization while SwiftComp runs in the background.
Solution Procedure
The problem is solved in the following three steps:
Part 1- Micro-scale analysis of the square-pack fiber matrix micro structure using Texgen4SC.
Part 2- Meso-scale analysis of the plain weave laminate using Texgen4SC.
Part 3- Macro-scale analysis of the Trac Boom using Abaqus CAE with the Abaqus SwiftComp GUI and SwiftComp 2.1.
Part 1- Micro-scale analysis of the square-pack fiber matrix micro structure using Texgen4SC.
Part 2- Meso-scale analysis of the plain weave laminate using Texgen4SC.
Part 3- Macro-scale analysis of the Trac Boom using Abaqus CAE with the Abaqus SwiftComp GUI and SwiftComp 2.1.
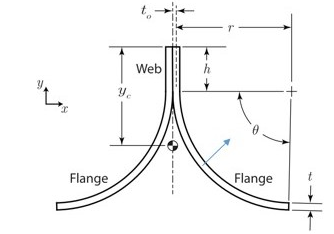
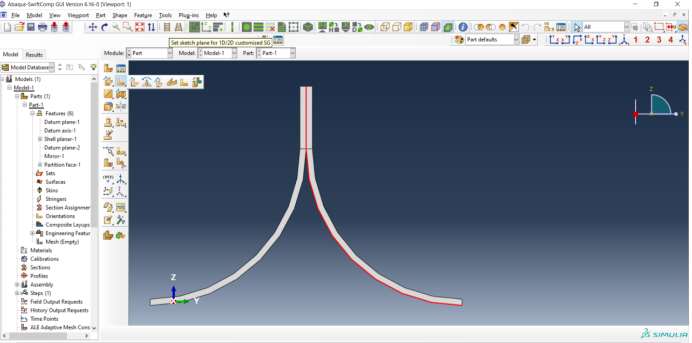
# Step 3.1. Using Abaqus CAE with the Abaqus SwiftComp GUI plugin, Create the part geometry for the TRAC Boom. Use Set sketch plane for customized SG -> Create planar shell -> Select the plane and vertical axis -> Sketch half of the base line (Highlighted as a red line). Its geometry is a straight line (Web height) from (0,10) to (0,0) and a curved line (Flange) from (0,0) to (25,-25) centered at (25,0). Set its thickness to 1 mm to the right of the baseline. Mirror the part about the vertical to get the geometry of the TRAC Boom. Partition the part to seperate the web and flange and also the individual flanges.
BR]
# Step 3.2. To enter the material properties for the part, first we need to choose the material properties from the results of the computed effective viscoelastic properties in the previous part. Within the Materials section of Abaqus CAE, we create a dummy material called “Material”. Please note that we will not define the material properties using the Abaqus SwiftComp GUI.
BR]
(Image(44.png, desc="dd") failed - File not found)
# Step 3.3.Import the material properties from the previous step
(Image(Tfdpng, desc="Material properties") failed - File not found)
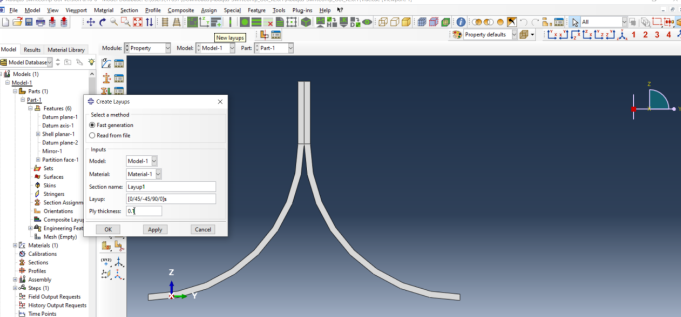
# Step 3.4. Now go to New Layups and add the material, section name, Layup and thickness to create the required layup. This can be repeated if we have multiple layups.
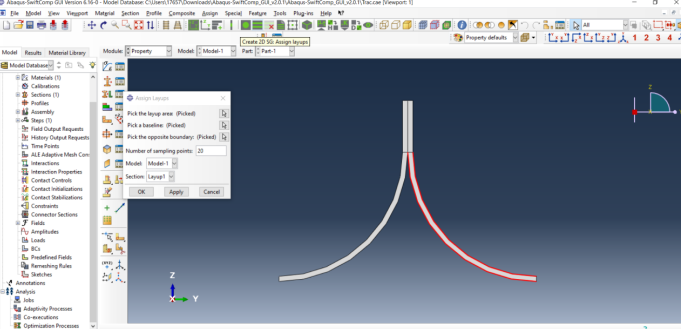
‘ # Step 3.5. To assing the layup, go to Create 2D SG: Assign Layups and the pick the baseline, the line opposite to the baseline and the area between the two picked line for the right flange as shown and then hit Ok. Do this for all four sections
‘ # Step 3.6. Now go to Assemble, create the part instance with dependent mesh.
(Image(T55.png, desc="asemblys") failed - File not found)
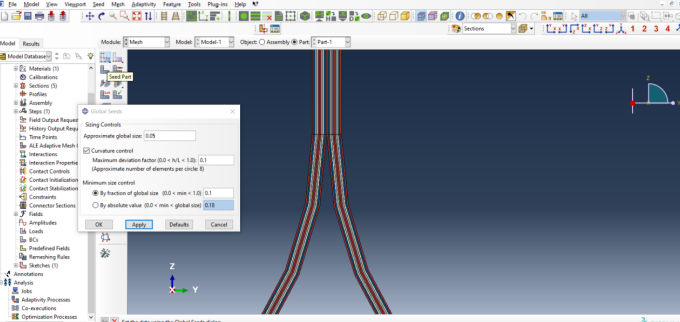
# Step 3.7.In the Mesh section, Seed the Part and set approximate global mesh size, then Click ‘Mesh Part’
# Step 3.8.Create a job and write its input file.
(Image(Tf.png, desc="ip file") failed - File not found)
# Step 12. Homogenize the part preferably as a 1D beam using the Homogenization via input file option to get the final results.
(Image(T33.png, desc="Homogenization") failed - File not found)
References
# Rique, O.; Liu, X.; Yu, W., Pipes, R. B.: “Constitutive modeling for time- and temperature-dependent behavior of composites,” Composites Part B: Engineering, Vol 184, March 2020, DOI: 10.1016/j.compositesb.2019.107726.