Prof. Yu's Research Group in the Cloud

Viscoelastic Homogenization with Time-dependent Constituent Properties

In this example, we want to compute the effective properties of a composite material made of isotropic viscoelastic matrix and transversely isotropic elastic fiber. The fiber properties are defined by means of engineering constants as specified in the table below.

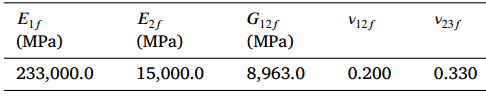Fiber properties defined as transversely isotropic elastic

The matrix properties are given as a time-dependent properties, which means that for each time a value of the Young’s modulus is given. In addition, we will consider that the matrix has a constant Poisson’s ratio equal to 0.37. We will create a text file to input the time-dependent material properties as follows.

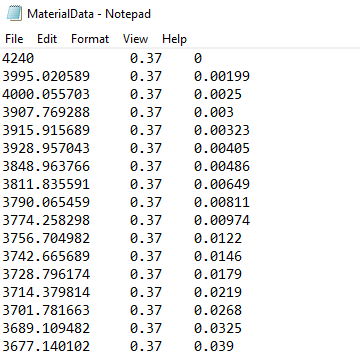Time-dependent matrix properties

Please note that for different viscoelastic anisotropies, the material properties should be defined as follows in different columns.

- Transversely isotropic. —- Young’s Modulus, E (t) —- Poisson’s ratio, nu (t) —- Time, t

- Orthotropic defined by means of engineering constants. —- E₁ (t) —- E₂ (t) —- E₃ (t) —- nu₁₂ (t) —- nu₁₃ (t) —- nu₂₃ (t) —- G₁₂ (t) —- G₁₃ (t) —- G₂₃ (t) —- Time, t

- Orthotropic defined by means of stiffness matrix. —- D₁₁₁₁ (t) —- D₁₁₂₂ (t) —- D₂₂₂₂ (t) —- D₁₁₃₃ (t) —- D₂₂₃₃ (t) —- D₃₃₃₃ (t) —- D₁₂₁₂ (t) —- D₁₃₁₃ (t) —- D₂₃₂₃ (t) —- Time, t

- Anisotropic. —- D₁₁₁₁ (t) —- D₁₁₂₂ (t) —- D₂₂₂₂ (t) —- D₁₁₃₃ (t) —- D₂₂₃₃ (t) —- D₃₃₃₃ (t) —- D₁₁₁₂ (t) —- D₂₂₁₂ (t) —- D₃₃₁₂ (t) —- D₁₂₁₂ (t) —- D₁₁₁₃ (t) —- D₂₂₁₃ (t) —- D₃₃₁₃ (t) —- D₁₂₁₃ (t) —- D₁₃₁₃ (t) —- D₁₁₂₃ (t) —- D₂₂₂₃ (t) —- D₃₃₂₃ (t) —- D₁₂₂₃ (t) —- D₁₃₂₃ (t) —— D₂₃₂₃ (t) — Time, t

We will use a square pack 2D SG with fiber volume fraction equal to v_f = 0.64.

Software Used

In his tutorial we will use Abaqus CAE with the Abaqus SwiftComp GUI plug-in. Abaqus CAE will be used to GUI to define the time-dependent material properties and to run the viscoelastic homogenization. SwiftComp will run in the background.

Solution Procedure

The steps required to compute the effective viscoelastic properties using Abaqus SwiftComp GUI are as follows.

# Step 1. We define the material properties in global coordinate system. We click on Materials in Abaqus CAE and define the Fiber properties by means of the engineering constants and click “Ok”.

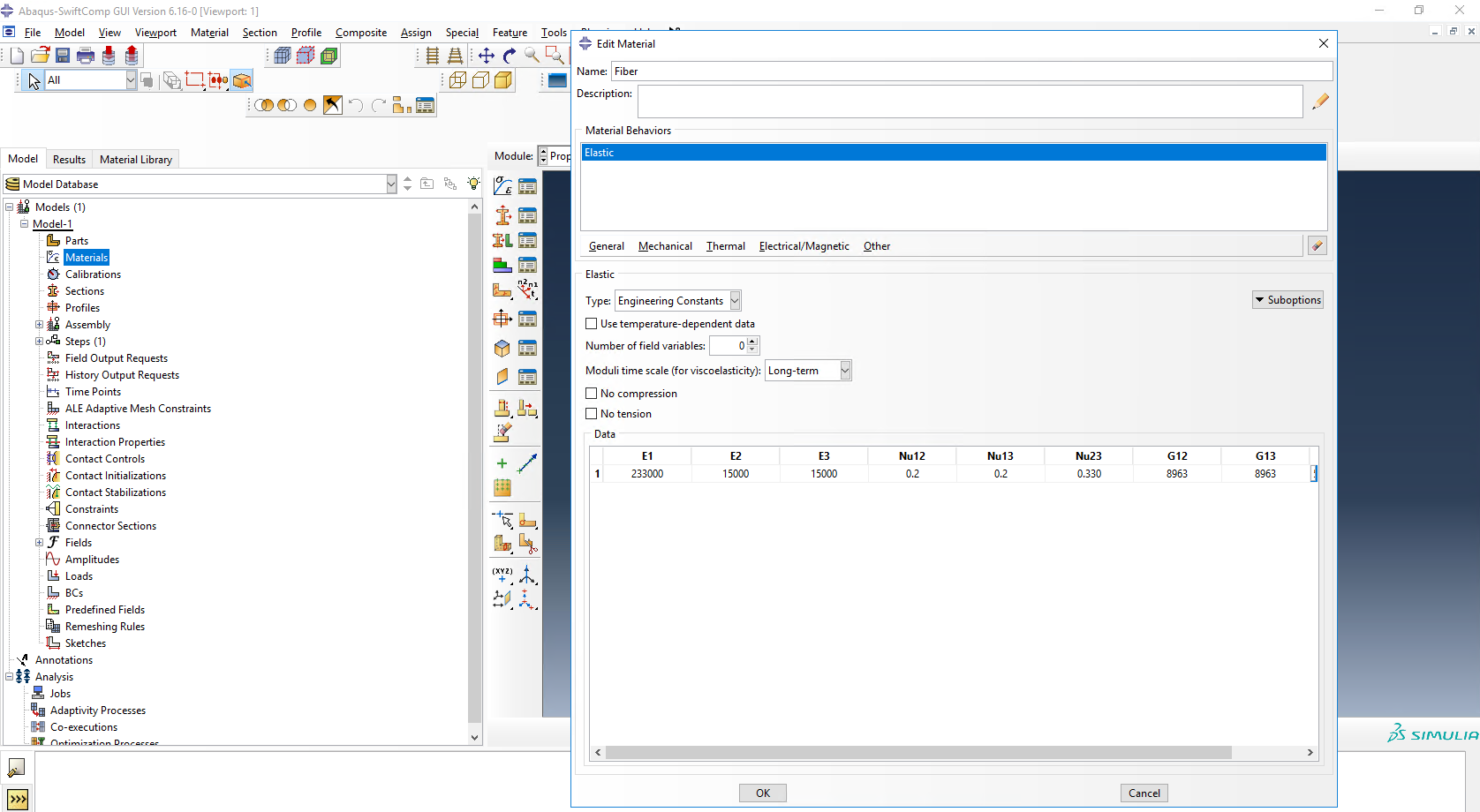Definition of the fiber properties

# Step 2. Within the Materials of Abaqus CAE, we create a dummy material called “Matrix”. Please note that we will not define the Prony coefficients of the resin using the Abaqus SwiftComp GUI in the next step.

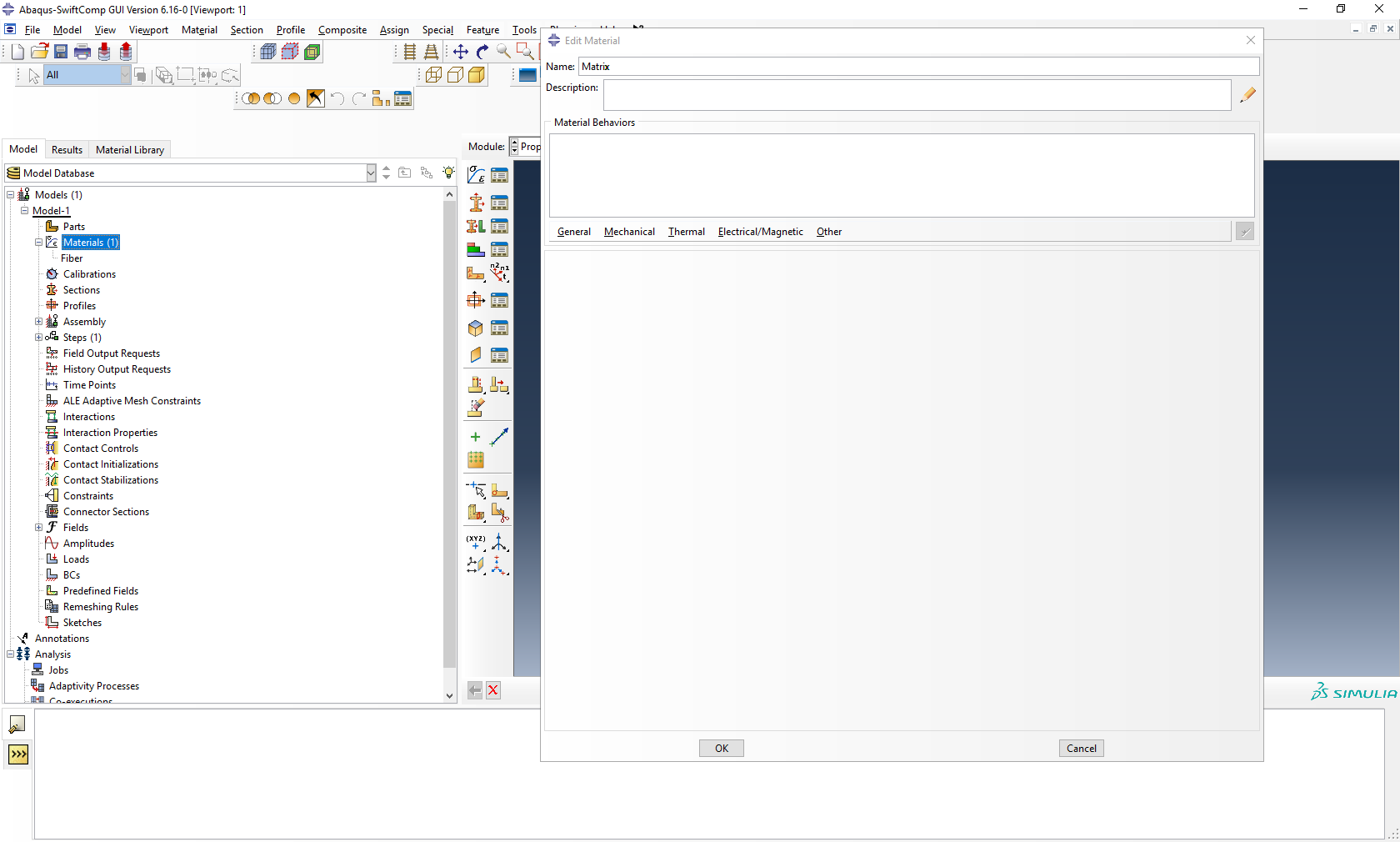Creation of the dummy material for the matrix

# Step 3. In the Abaqus SwiftComp GUI menu, we click on Input Time-Dependent Properties. We select “Time-dependent” and “Viscoelastic” in the Method & Analysis section. We pick “Matrix” as the Material to be modified in the drop down menu. Then, we look for the text file used to input the material properties. This text file can be located in any folder of the computer. Finally, we click the two “Ok“s as shown in the picture.

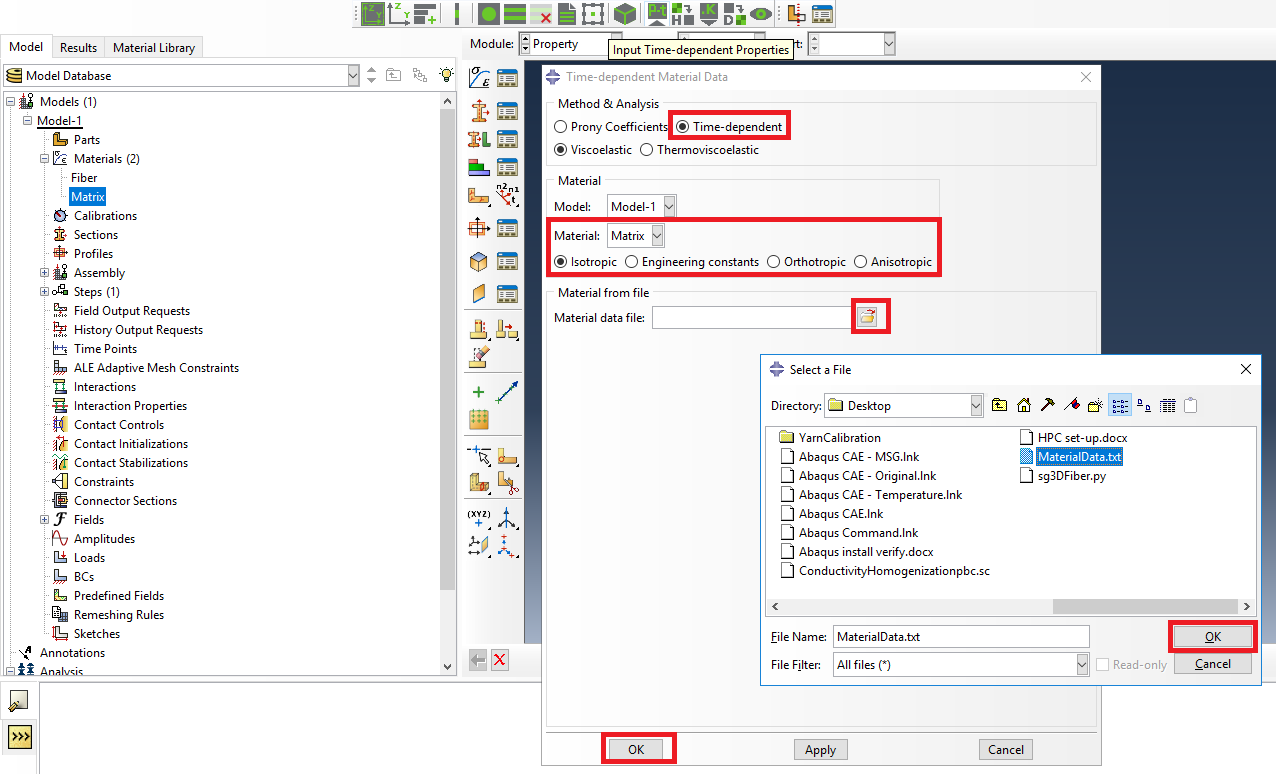Definition of the matrix Prony coefficients

# Step 4. From the default the Abaqus SwiftComp GUI SGs, we pick the 2D Structure Genome with Square pack. We input the fiber volume fraction, define the approximate global mesh size, and click “Ok”. A square pack microstructure will be automatically generated.

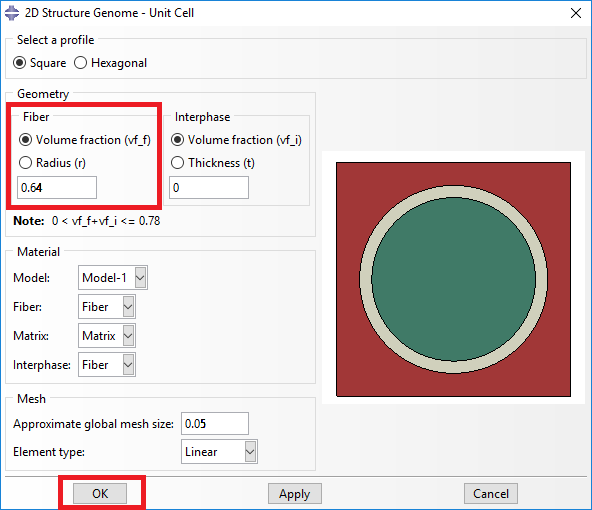Definition of the 2D SG square pack microstructure

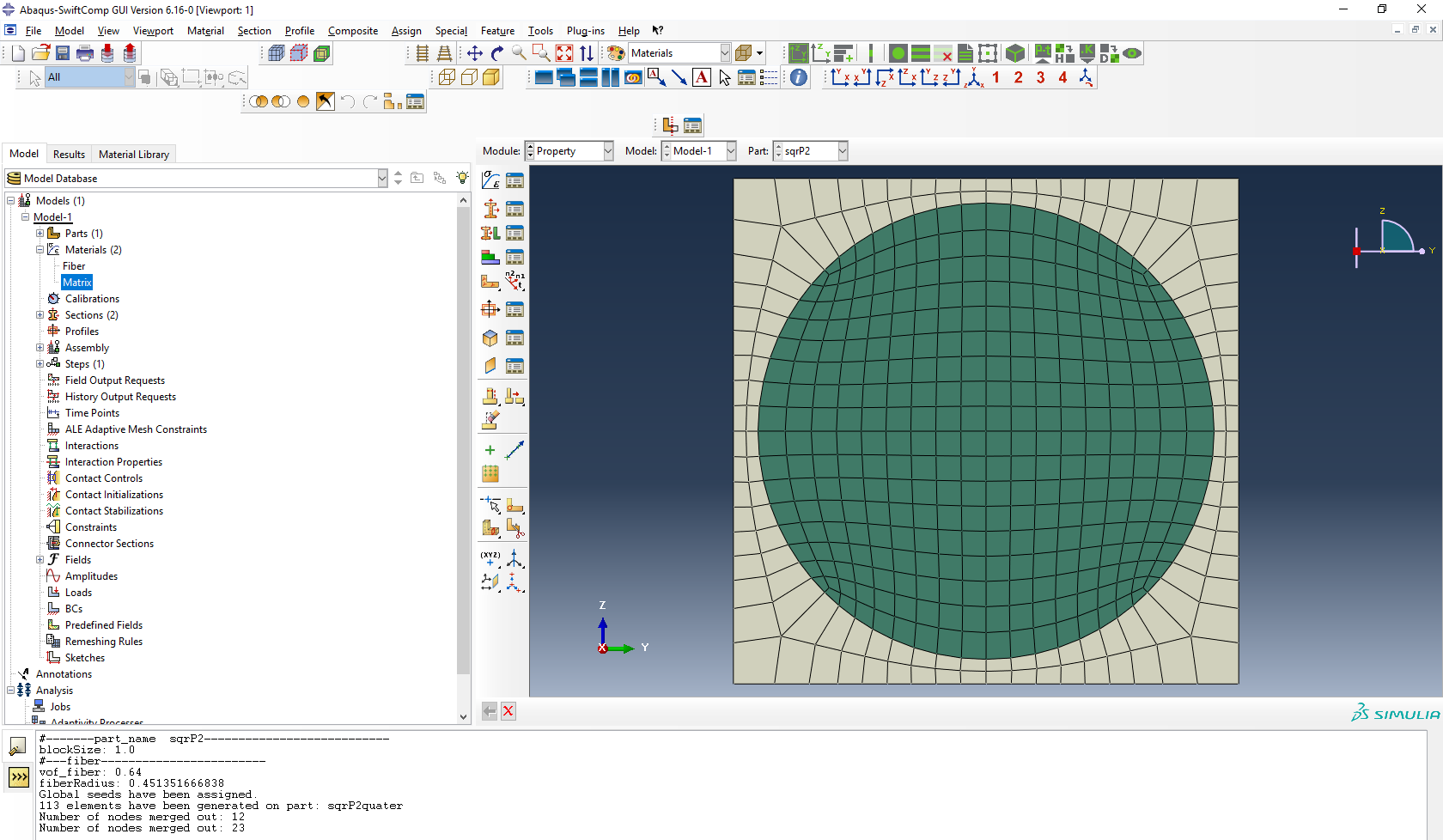2D SG square pack microstructure

# Step 5. Now, we will compute the effective viscoelastic properties. To do so, we click on Homogenization and select Viscoelastic in Analysis Type. In the Viscoelastic/Thermoviscoelastic Analysis section, we define the range of the time (i.e. Initial time” and Final time”) in which we want to output the effective properties as well as the frequency (i.e. Time increment” defined in decades).

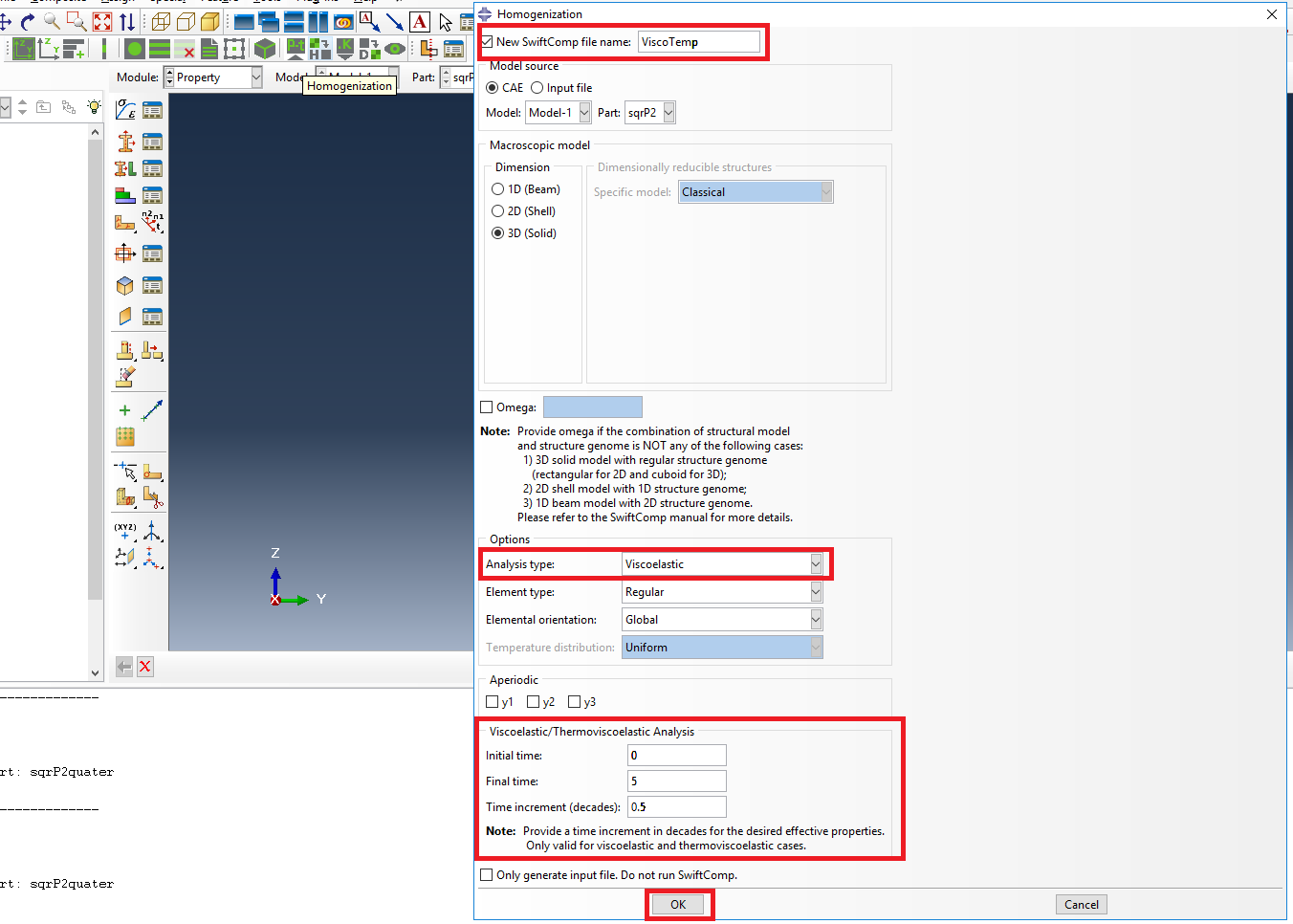Definition of the viscoelastic homogenization step

# Step 6. We click on Ok to run the homogenization step. SwiftComp on the background will run the homogenization.

SwiftComp running on the background

# Step 7.The results can be found in the .sc.k file as shown next. Note that the effective properties will be outputted for each specified time.

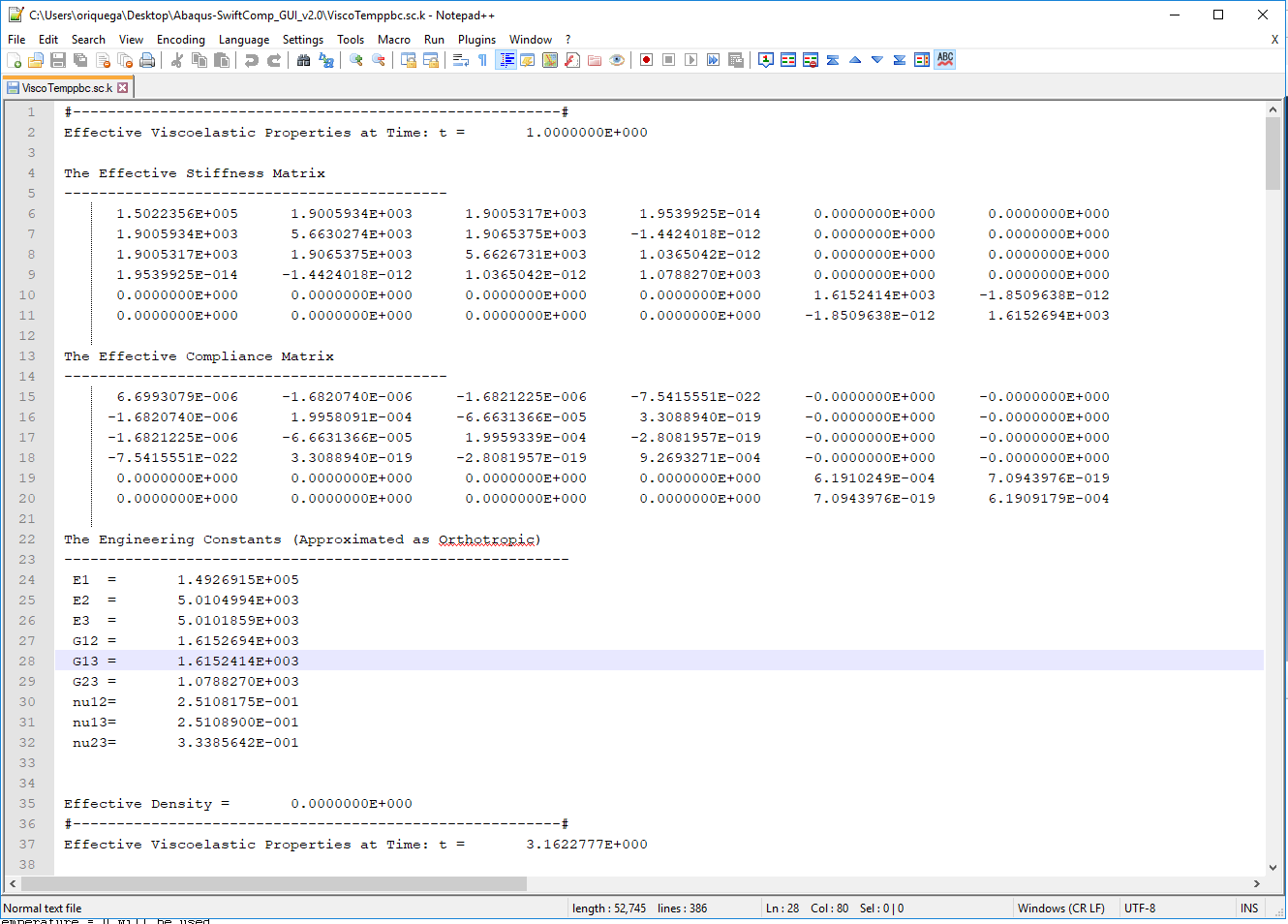Results corresponding to the effective viscoelastic properties

The MSG solid model is used to predict the effective thermoelastic properties of a plain weave composite by taking the effective yarn properties and matrix properties to predict the effective properties of weave composites. Software Used

The example will be solved using the TexGen4SC 2.0. Solution Procedure

Below describe the detailed step by step procedure you followed to solve the problem.

# Step 6 Create mesoscale plain weave SG with the yarn geometries given as

# Step 7 Create plain weave pattern as

# Step 8 Go to Homogenization->Microscale and select thermoelastic analysis. Keep the default material properties. The fiber volume fraction 0.64 as
Click finish and the microscale homogenization will be performed and the results will be automatically pop up. Note

# Step 9 The effective yarn properties will be automatically assigned to the mesoscale model. However, users need to define the matrix properties for the mesoscale model. Usually, the matrix at the mesoscale is the same as the one at microscale as shown
(Image(l5.PNG) failed - File not found)

# Step 10 Go to File->Export->SwiftComp File, define the voxel mesh and run elastic analysis using the MSG solid model
(Image(l6.PNG) failed - File not found) Save the sc file and click to the Homogenization->Mesoscale. The effective properties of the plain weave composite will be automatically pop up
(Image(l7.PNG) failed - File not found)

1. Step 11 .We move on to macroscopic homogenization of the Lenticular boom.

(Image(l188.PNG) failed - File not found)

# Step 12.Go to Module > Property > Create Material and create a material with the properties obtained in the previous step.
(Image(l8.PNG) failed - File not found)

# Step 13.’We move on geometry and create the cross section from Module > Property > Create Section . Create a section, Layup-1, shown as below with Solid-Composite. Note here that the thickness of each layer should be actual thickness instead of relative thickness.

(Image(l10.PNG) failed - File not found)

# Step 14.To create the geometry, in the SwiftComp Toolset, click the “Set sketch plane for 1D/2D customised SG” and secelt the 2D option. In the toolbox of the Part module, click ‘Create Shell: Planar’ , following the prompt, select the datum plane and the datum axis. Sketch the shape shown below. Click ‘Done’, then the part will be generated sketch planesketch plane

(Image(l11.PNG) failed - File not found)

# Step 15.First we will assign the layup for the segment on the right. Make the two partition as shown and Click ‘Assign Layups’ in the SwiftComp toolset. Pick the area in the right, pick the appropriate baseline and select section ‘Layup-1’. Click ‘OK’. Repeat the step for all segments.
(Image(l12.PNG) failed - File not found)

# Step 16.To assign local coordinates, go to Module > Property > Assign Material Orientation Following the prompt, we first select the top segement to be assigned a local material orientation, and click ‘Done’. Then in the prompt area, click ‘Use Default Orientation or Other Method’ button. In the ‘Edit Material Orientation’ dialog box, select ‘Discrete’ as the Orientation Definition. Then click , open the ‘Edit Discrete Orientation’ dialog box. In the Normal axis definition choose Vector (i,j,k), and set the vector (1.0, 0.0, 0.0). For Primary Axis, choose 1 as the Primary axis direction and Edges as the Primary axis definition. Click to select the light blue edge shown in the figure below, then click ‘Done’. Use Flip Direction to make the axis pointing to the right if necessary. Click ‘Continue…’ then ‘OK’ to finish this assignment. Same procedure for the rest three segments. Some steps may not be exactly the same. The only requirement is to make sure that the asix 2 pointing outwards. material orientation
(Image(l13.PNG) failed - File not found) # Step 17. Module > Mesh > Seed Part and choose mesh size, then Click ‘Mesh Part’
(Image(l14.PNG) failed - File not found) # Step 18. Homogenize the part to get the final results.
(Image(l15.PNG) failed - File not found)

(Image(l20.PNG) failed - File not found)

References

1. Liu, X.; Tang, T.; Yu, W., Pipes, R. B.: “Multiscale modeling of viscoelastic behavior of textile composites,” International Journal of Engineering Science, Vol 130, September 2018, pp. 175-186, DOI: 10.1016/j.ijengsci.2018.06.003.

1. Rique, O.; Liu, X.; Yu, W., Pipes, R. B.: “Constitutive modeling for time- and temperature-dependent behavior of composites,” Composites Part B: Engineering, Vol 184, March 2020, DOI: 10.1016/j.compositesb.2019.107726.

Created on 31 Mar 2020, Last modified on 16 Jul 2020