Problem Description
The MSG solid model is used to predict the effective properties of a plain weave composite using a two-step approach. This problem is the first example in the paper “Liu, X., Rouf, K., Peng, B. and Yu, W., 2017. Two-step homogenization of textile composites using mechanics of structure genome. Composite Structures, 171, pp.252-262.”
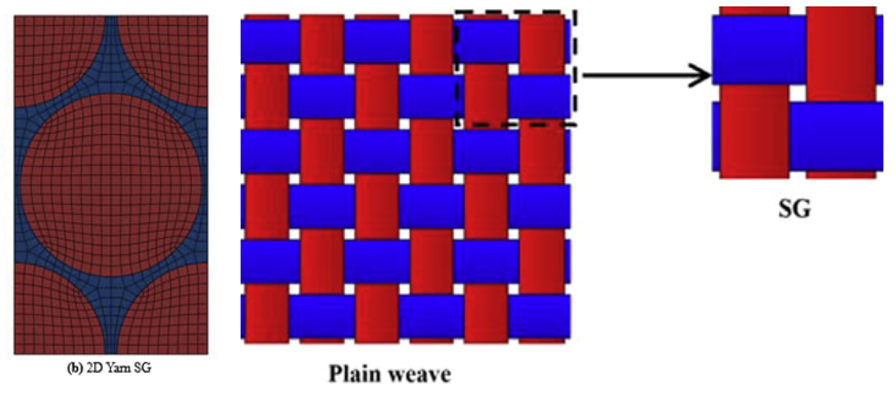
The first step predicts the effective yarn properties based on the fiber and matrix properties at the microscale. The second step takes the effective yarn properties and matrix properties to predict the effective properties of weave composites. The microscale and mesoscale models are given as
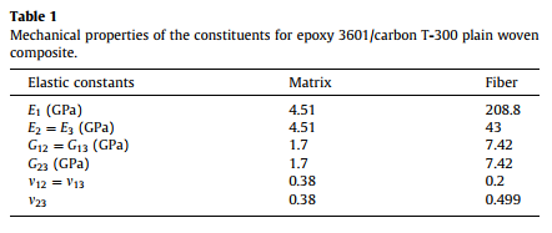
The fiber and matrix properties are given as
The youtube video of this problem can be obtained
https://youtu.be/bsPJ_8lxZn8
Software Used
The example will be solved using the TexGen4SC 2.0.
Solution Procedure
Below describe the detailed step by step procedure you followed to solve the problem.
* step1 Create mesoscale plain weave SG with the yarn geometries given as
* step 2 Create plain weave pattern as
* step 3 Go to Homogenization->Microscale to select the hexagonal micromechanical model and define the elastic properties of fiber and matrix and fiber volume fraction 0.8 as
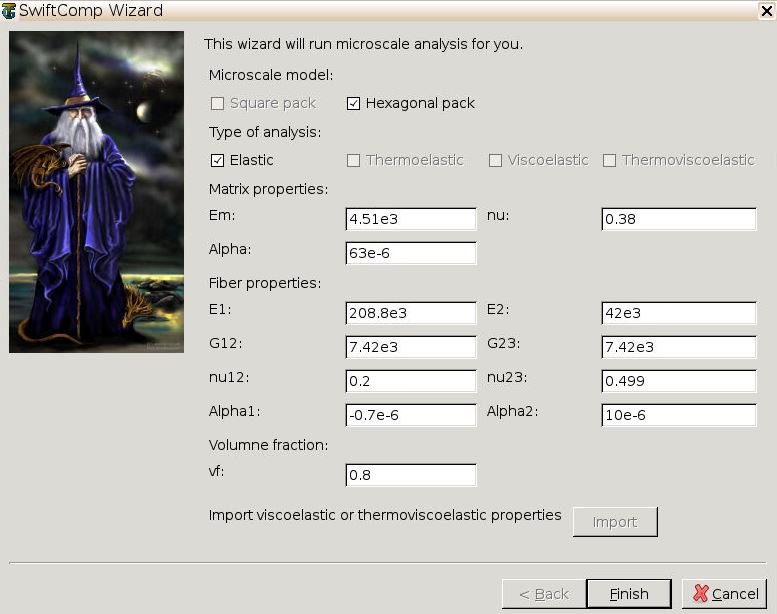
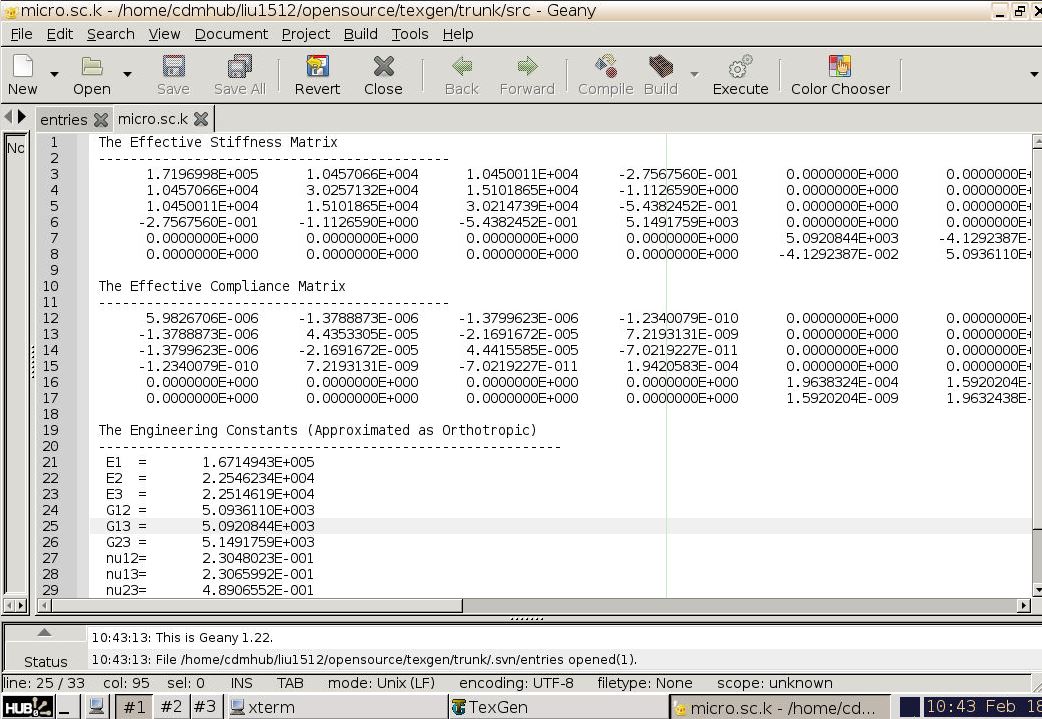
Note the CTEs will not be used for the elastic analysis. Click finish and the microscale homogenization will be performed and the results will be automatically pop up
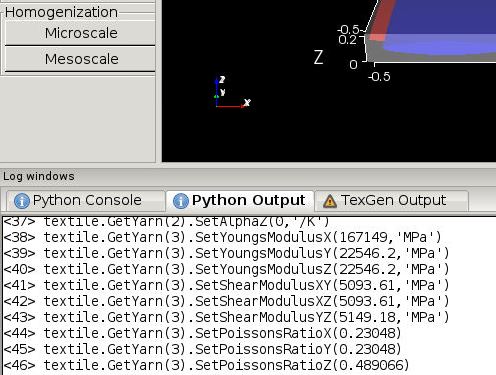
* step 4 The effective yarn properties will be automatically assigned to the mesoscale model as shown
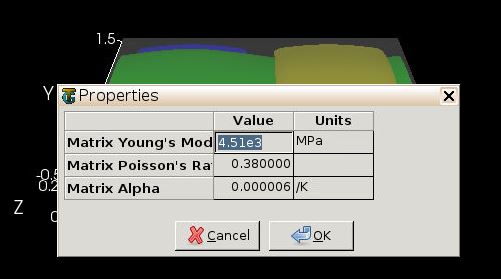
However, users need to define the matrix properties for the mesoscale model. Usually, the matrix at the mesoscale is the same as the one at microscale as shown
* step 5 Go to File->Export->SwiftComp File, define the voxel mesh and run elastic analysis using the MSG solid model
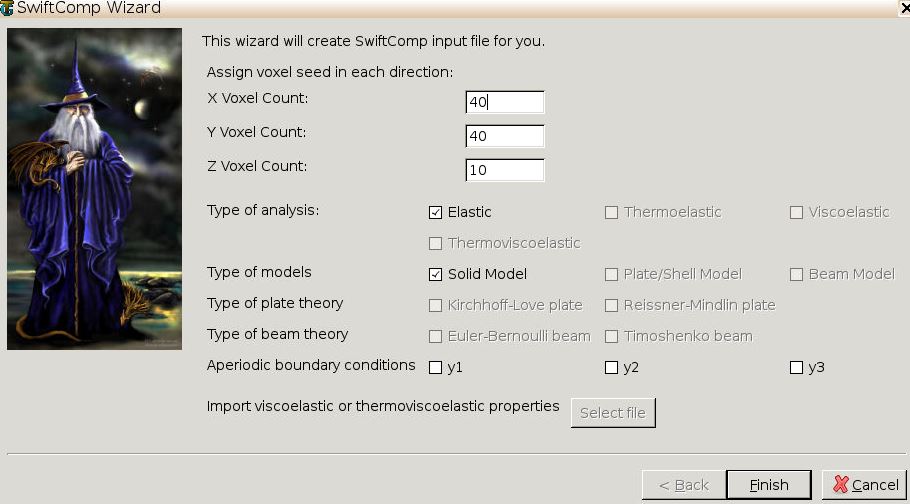
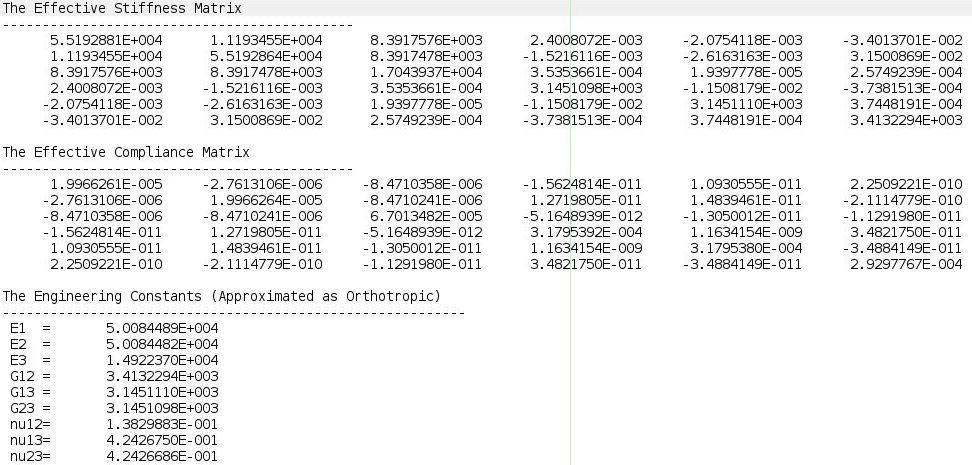
Save the sc file and click to the Homogenization->Mesoscale. The effective properties of the plain weave composite will be automatically pop up
References
- Liu, X., Rouf, K., Peng, B. and Yu, W., 2017. Two-step homogenization of textile composites using mechanics of structure genome. Composite Structures, 171, pp.252-262.