Search
Search
Menu
Close

Prof. Yu's Research Group in the Cloud

Wiki

Main Page / Gmsh4SC tutorials /

Effective Properties of Hex-pack, Square-pack and Spherical-inclusion Microstructures

Search

Search pages

Wiki

Tools

Descriptions

In this wiki tutorial, you will learn about how to obtain effective properties of composites possessing four microstructures, including

  1. hexagonal packed fibers
  2. square packed fibers with interphase layer between fiber and matrix
  3. 0/90 laminate
  4. two spheres included in matrix

Geometric dimensions and material properties are taken from Challenge Problems for the Benchmarking of Micromechanics Analysis. Apart from how to calculate effective material properties of these four microstructures, you will also learn about

  • how to extract and plot local stress values along a line after dehomogenization (in Case 2)
  • how to draw a sphere and assign material properties by editing command files (in Case 4)

Software Used

Gmsh4SC 2.0

Case 1. Hexagonal Pack Microstructure

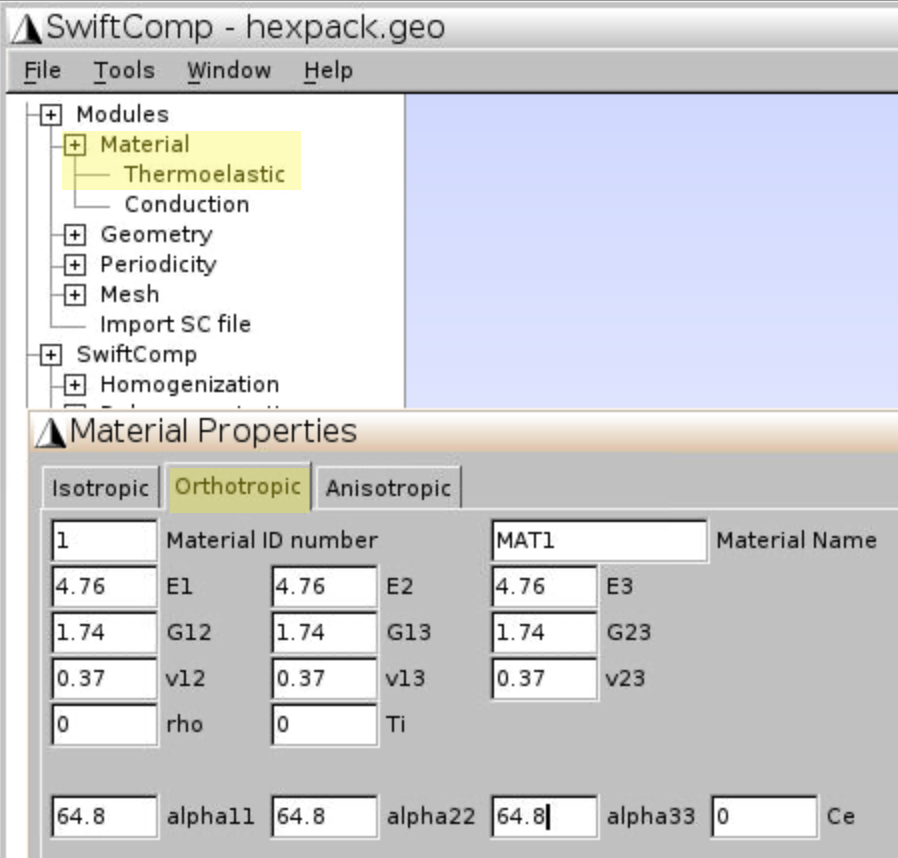
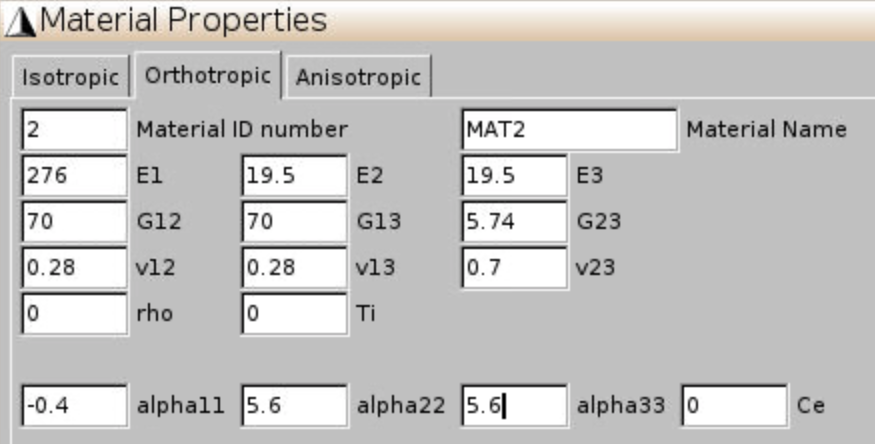
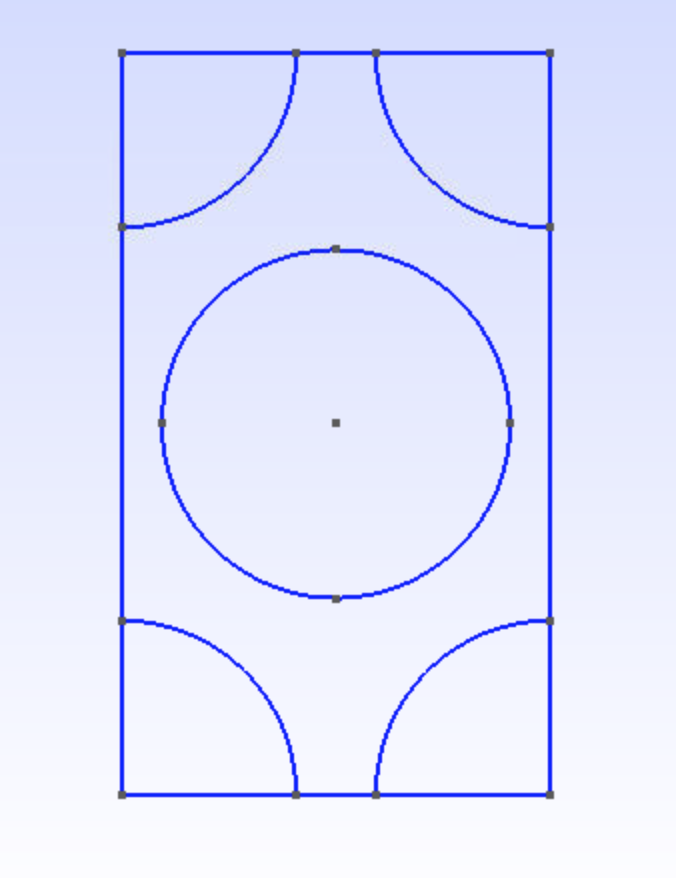
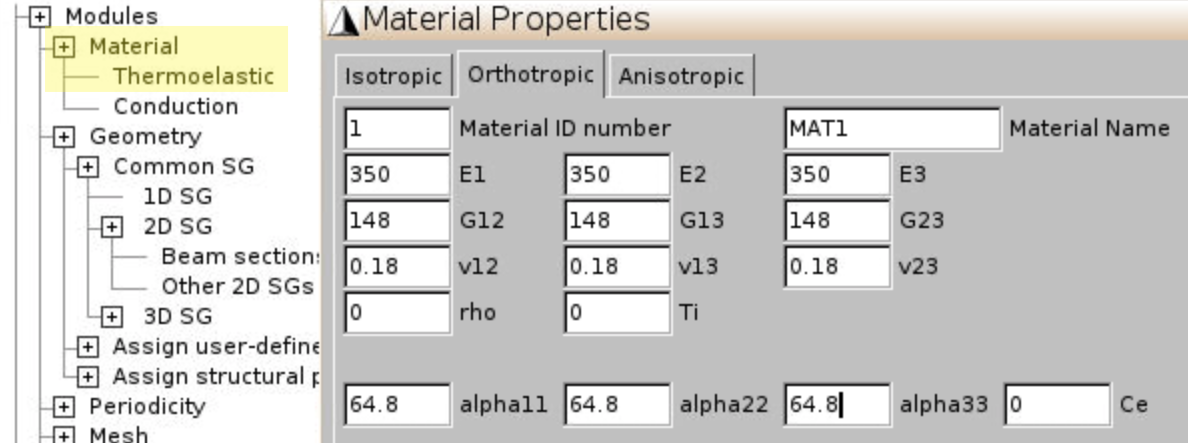
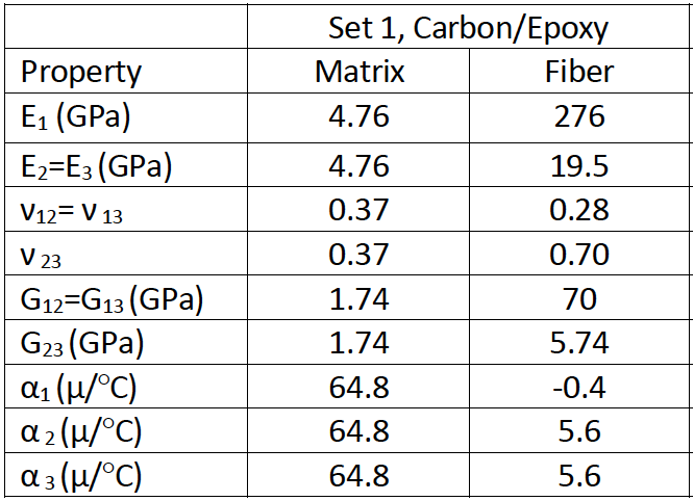
The hex pack microstructure describes a continuous fiber reinforced composite. Figure 1 shows the cross-section. Dark portion represents fiber. Volume fraction of fiber is 60%. Material properties are given in Figure 2.
Fig1_hexpack.png Fig2_Materials.png

Video

You may refer to the YouTube video for hex pack micromechanics analysis.

Solution Procedures

  • Launch Swift Comp.
  • Create a new file.
    Fig3_newfile.png
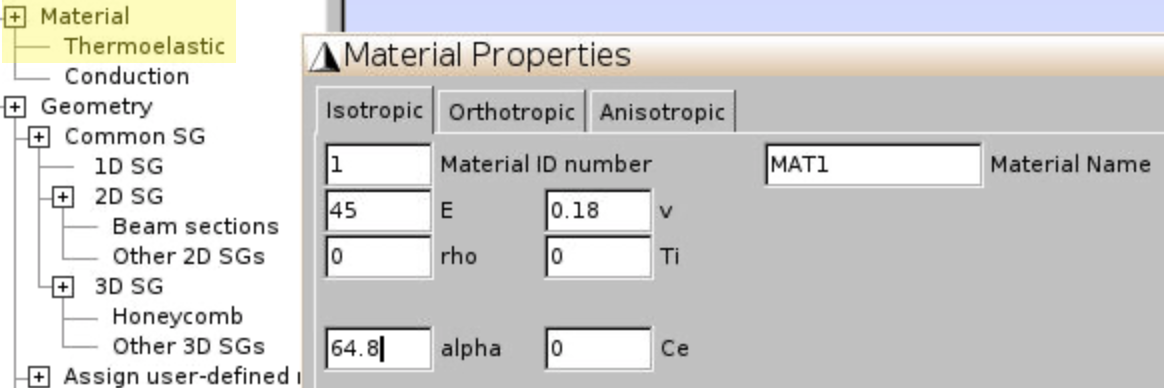
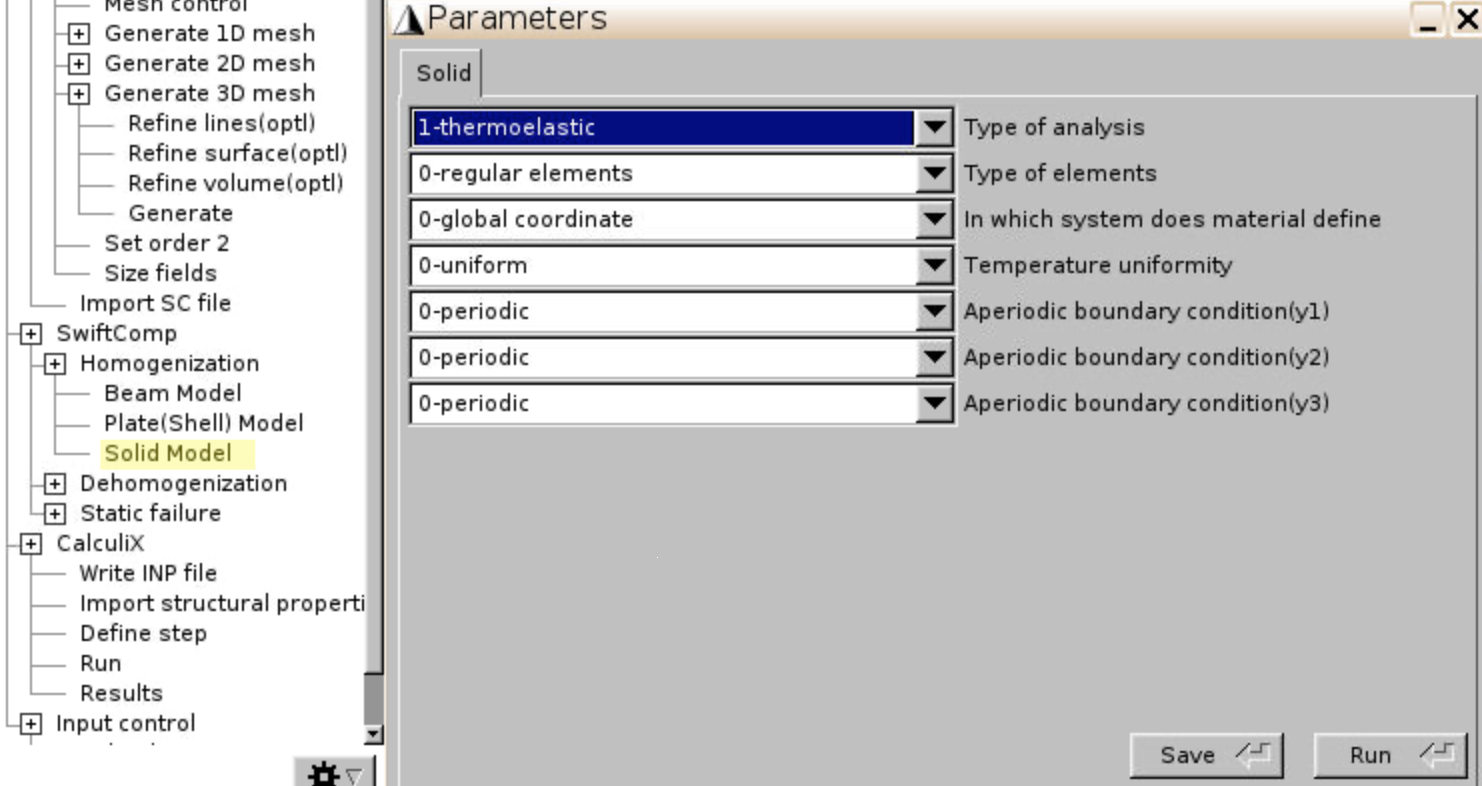
  • Add material properties
    • Click Material, Thermoelastic, Orthotropic, input matrix and fiber properties given in Figure 2, click Add for each material. Finally click Close.
      Fig4_Mat1.png Fig5_Mat2.png
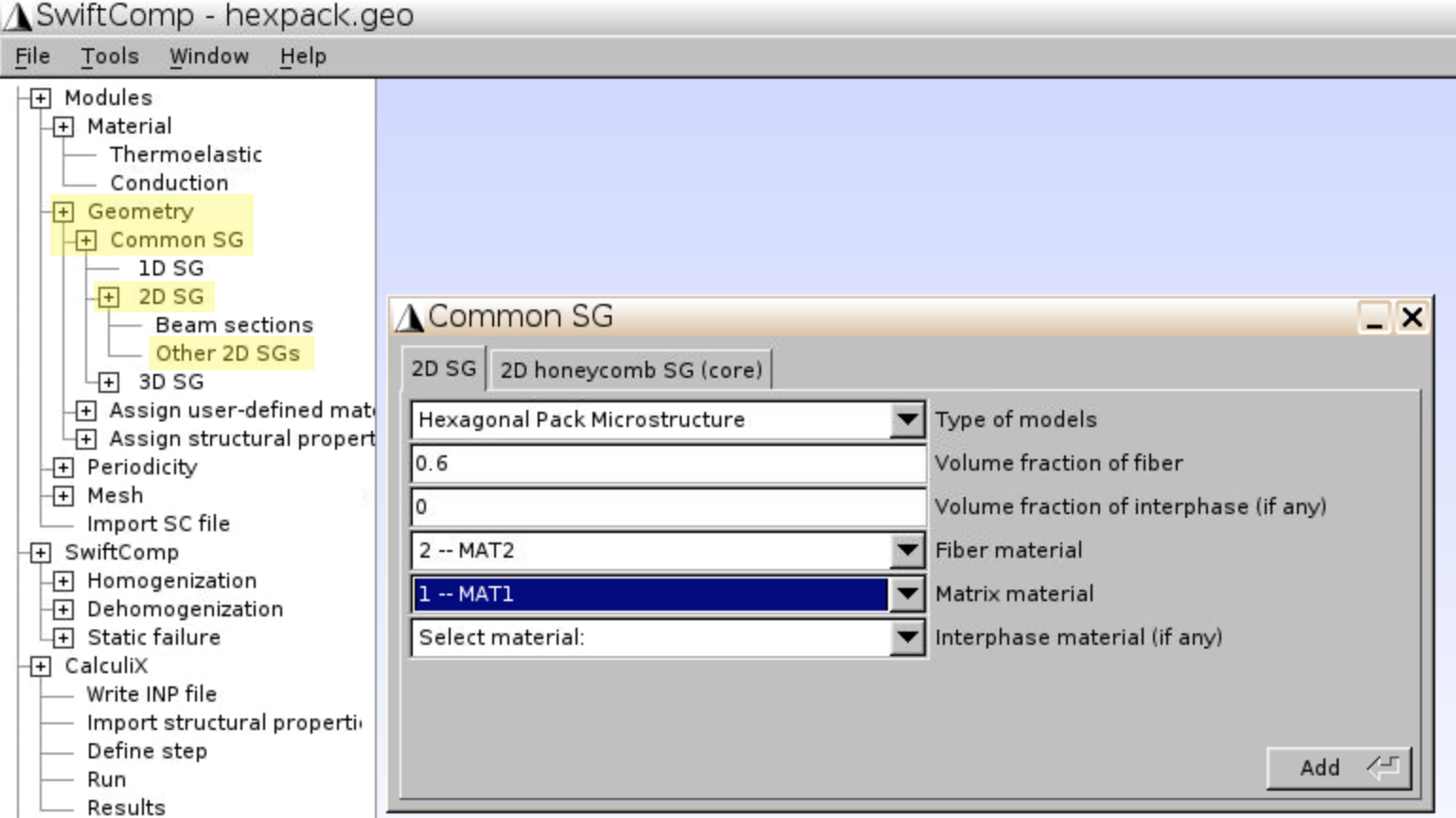
  • Define SG geometry
    • Click Geometry, Common SG, 2D SG, Other 2D SGs.
    • Select Type of models: Hexagonal Pack Microstructure, input Volume fraction of fiber: 0.6, select Fiber and Matrix materials to be MAT2 and MAT1, click Add. The hex pack geometry is generated as shown in Figure 7.
      Fig6_Geometry.png Fig7_Geometry2.png
  • Mesh
    • Click Mesh, Generate 2D mesh, Generate.
    • Click Set order 2.
      Fig8_Mesh.png Fig9_Meshorder2.png
  • Homogenization
    • Click SwiftComp, Homogenization, Solid Model
    • Select 1-thermoelastic as Type of analysis
    • Click Save, Run.
      Fig10_homogenization.png
    • The effective elastic properties and CTEs of the homogenized hex pack structure is given in Figure 11.
      Fig11_results.png

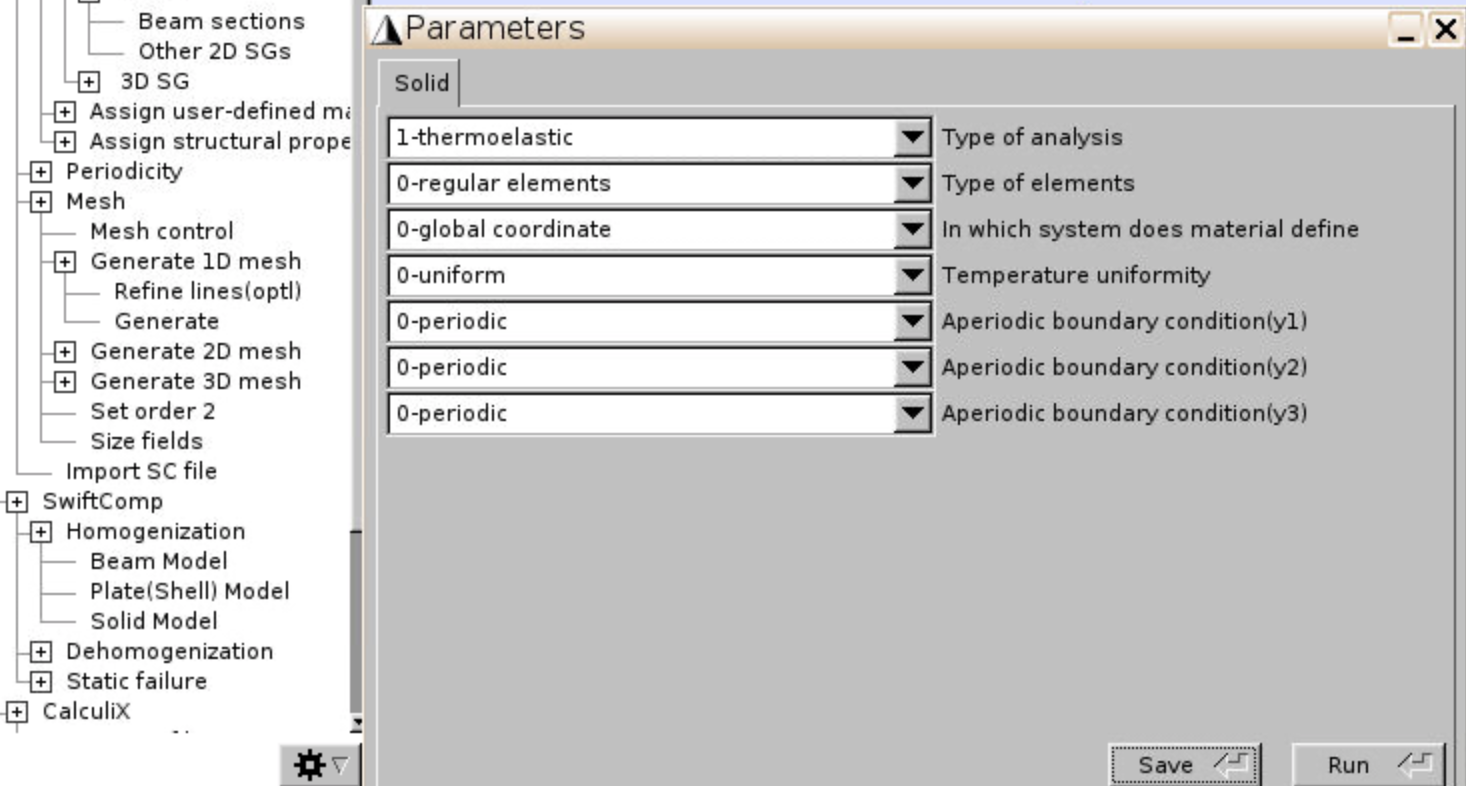
Case 2. Square Pack Microstructure

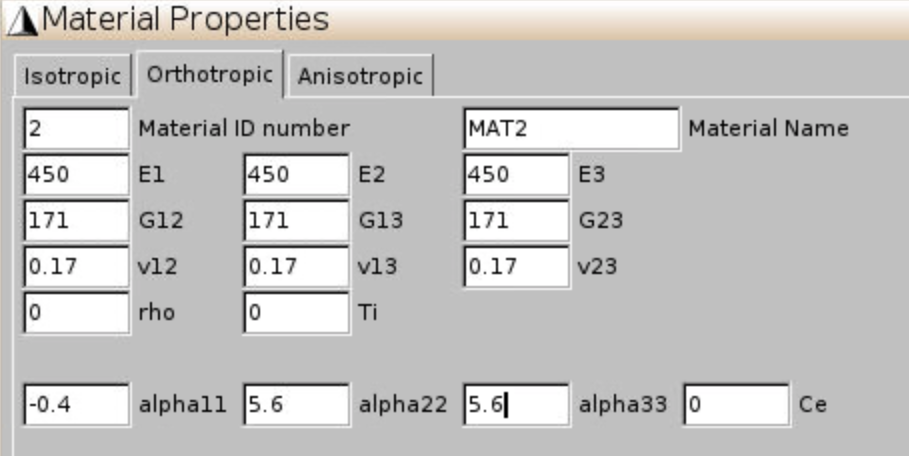
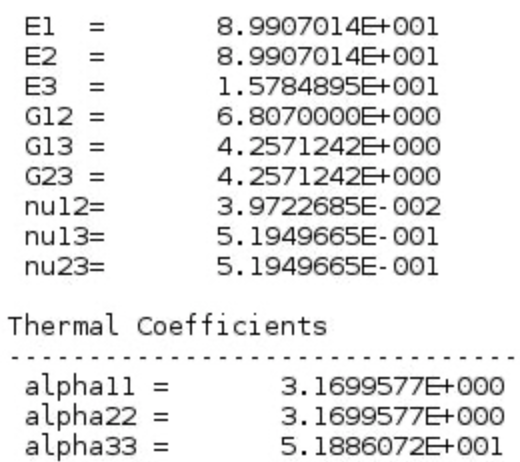
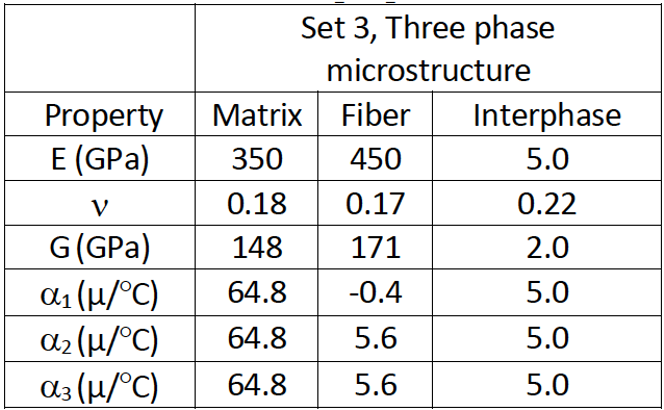
Cross section of a square pack composite with an interphase layer is given in Figure 12. Volume fraction of fiber and interphase is 60% and 1% respectively. Material properties are given in Figure 13.
Fig12_squarepack.png Fig13_Material.png

Solution Procedures

  • Add material properties
    • Click Material, Thermoelastic, Orthotropic, input the 3 material properties, click Add for each material. Finally click Close.
      Fig14_Mat1.png Fig15_Mat2.png Fig16_Mat3.png
  • Define SG geometry
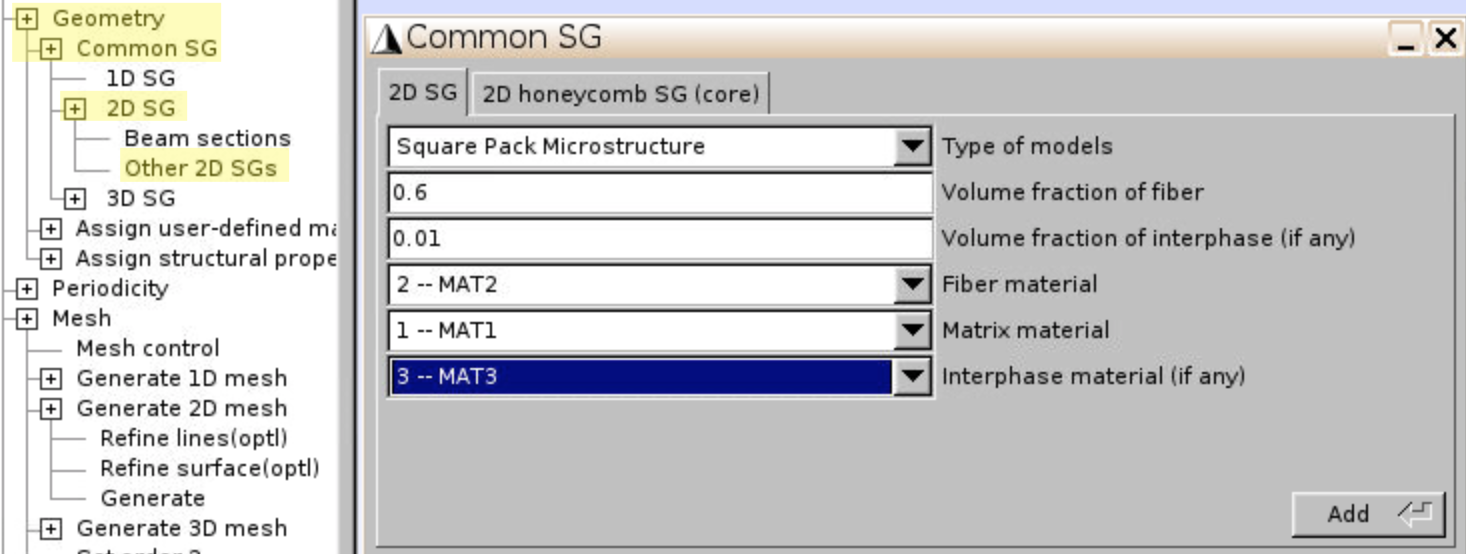
    • Click Geometry, Common SG, 2D SG, Other 2D SGs.
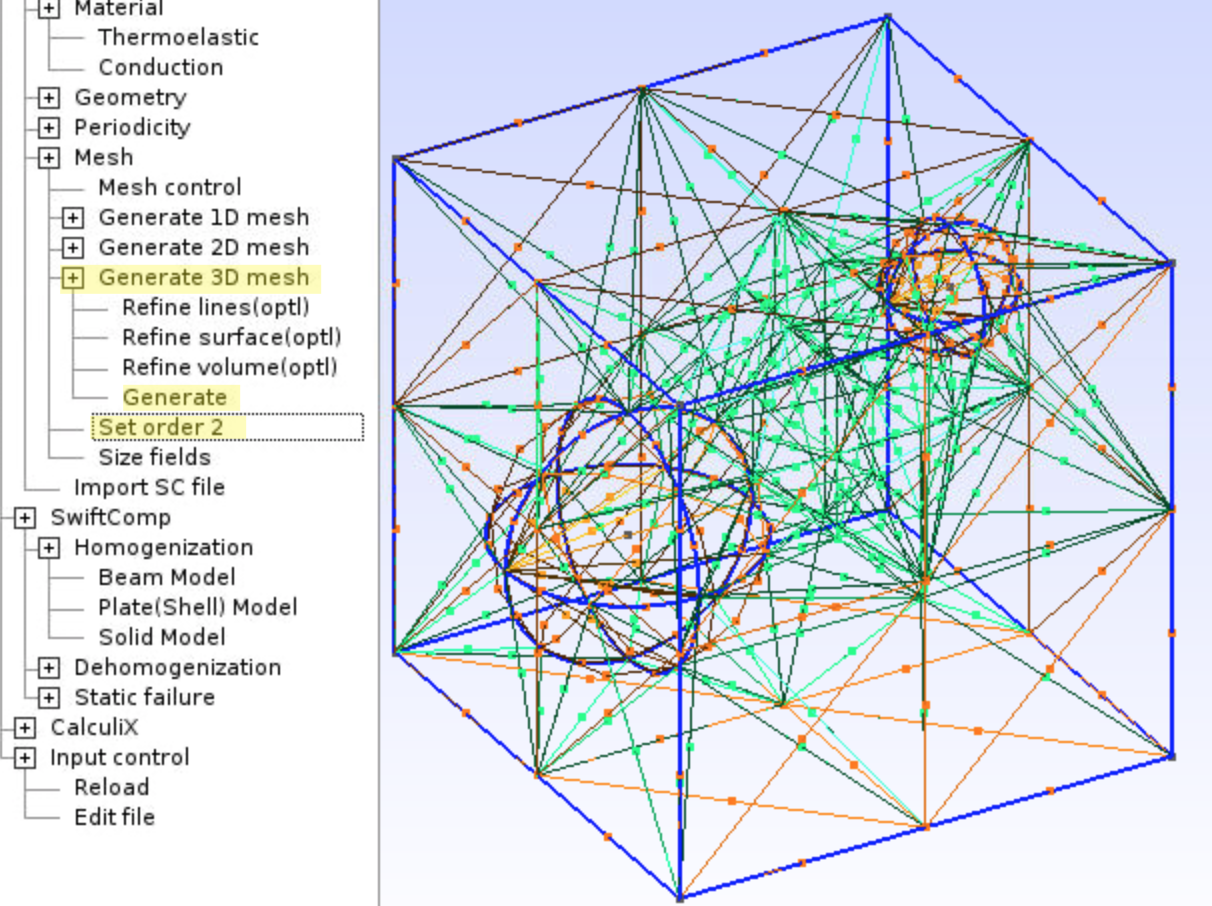
    • Select Type of models: Square Pack Microstructure, input Volume fraction of fiber: 0.6, Volume fraction of interphase: 0.01, select materials, click Add. The square pack geometry is generated as shown in Figure 18.
      Fig17_Geometry.png Fig18_GeometryVIEW.png
    • You may find the radii of fiber and interphase circles in Input control, Edit file.
      Fig19_radius.png
  • Mesh
    • As the interphase is very thin, we refine the mesh for circle arcs surrounding interphase layer.
    • Click Mesh, Generate 2D mesh, Refine lines.
    • Input Number of points: 50
    • Click the 8 circle arcs.
    • Press e, and q.
      Fig20_refinemesh.png
    • Click Generate 2D mesh, Generate.
      Fig21_mesh.png
  • Homogenization
    • Click SwiftComp, Homogenization, Solid Model
    • Select 1-thermoelastic as Type of analysis
    • Click Save, Run.
      Fig22_homogenization.png
    • The effective elastic properties and CTEs of the homogenized square pack structure is given in Figure 11.
      Fig23_results.png
  • Dehomogenization
    • Since we do not know the actual deformations, here we only show the representative local stress field, such as $$\sigma_{11}$$ distribution across the cross section under $$\epsilon_{11} = 1$$ loading.
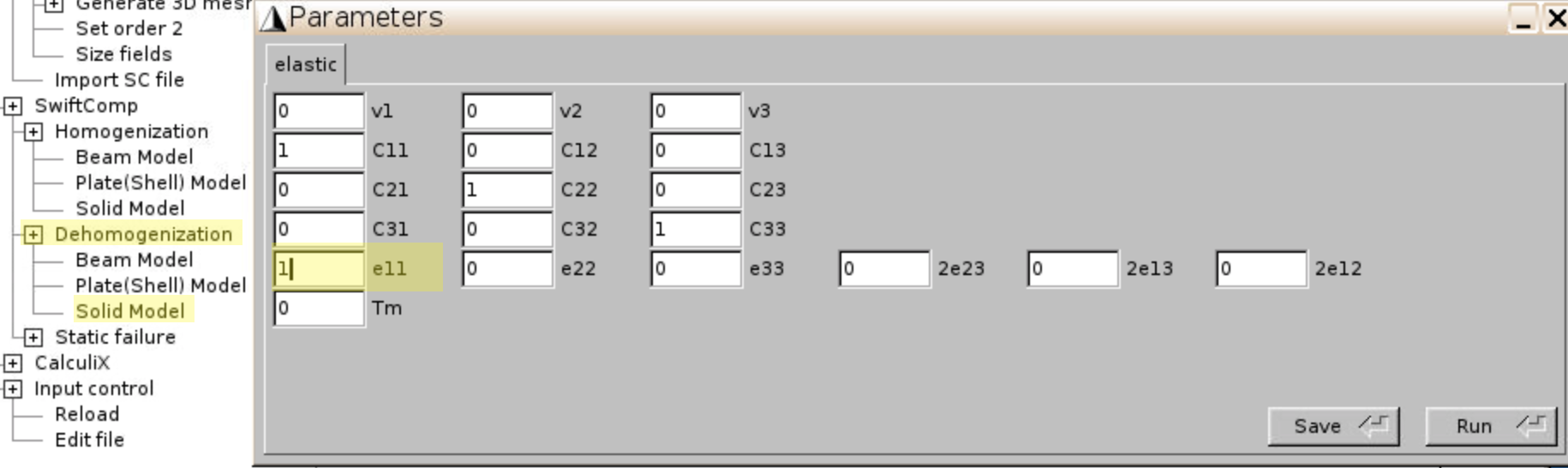
    • Click Dehomogenization, Solid Model.
    • Input 1 for e11.
    • Click Save, and Run.
      Fig24_s11undere11.png
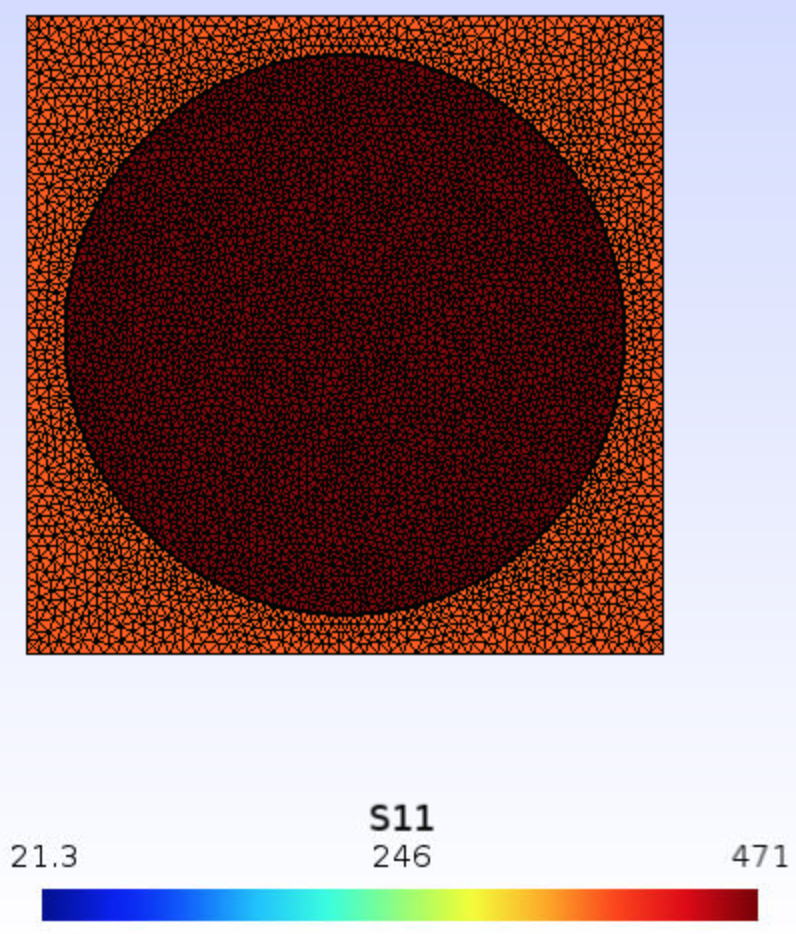
    • Axial stress $$\sigma_{11}$$ shows symmetric distribution across the cross section.
      Fig25_s11.png
    • Zoom in to check the interface layer.
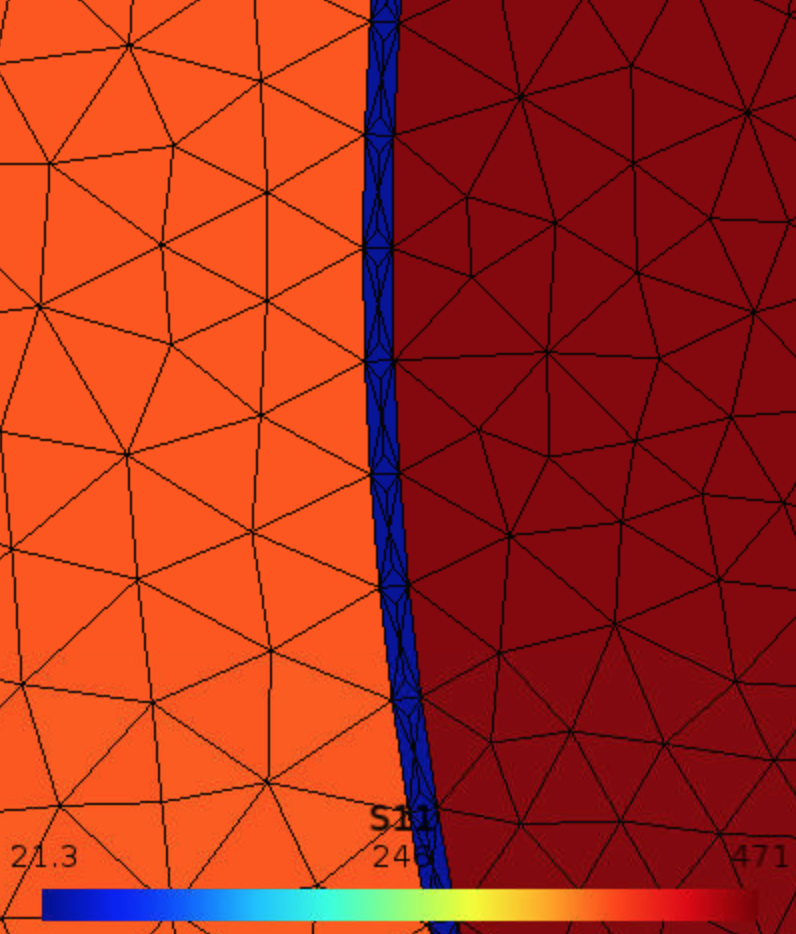
      Fig26_s11interface.png
  • Plot $$\sigma_{11}$$ along the center line
    • Click the triangular arrow beside S11, click Plugins.
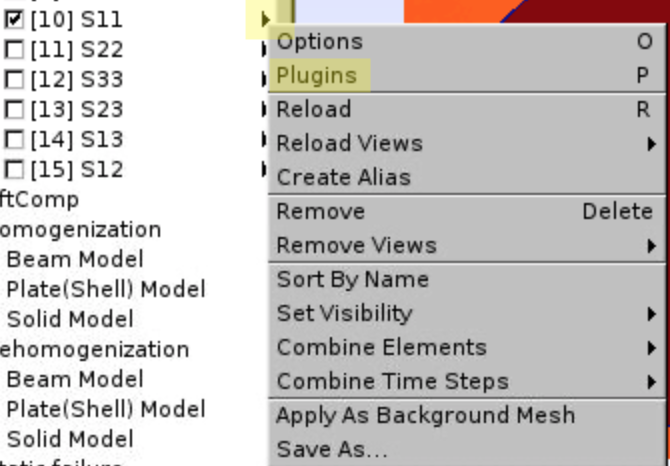
      Fig27_Plugin.png
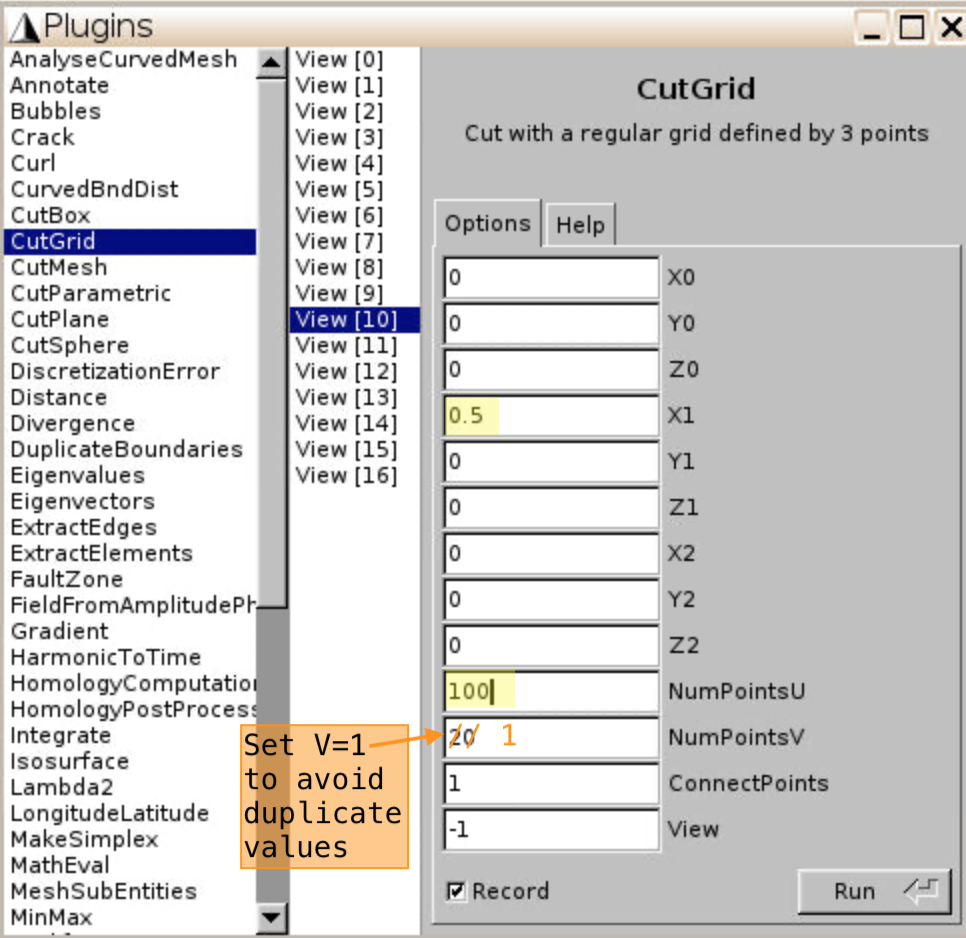
    • Choose CutGrid for View[10] (S11)
    • Set (X0, Y0, Z0) = (0, 0, 0), (X1, Y1, Z1) = (0.5, 0, 0), NumPointsU = 100 (or larger). This will create a cut from (0, 0, 0) to (0.5, 0, 0) using 100 points.
    • (X2, Y2, Z2) is set to be the same as (X0, Y0, Z0) to avoid additional points of no interest here.
    • The other side, e.g., from (-0.5, 0, 0) to (0, 0, 0), is symmetric.
      Fig28_CutGrid.png
    • Click Run. You’ll see a new View called S11_CutGrid.
    • Save the new view as .txt file by clicking the triangle arrow and choose Save As....
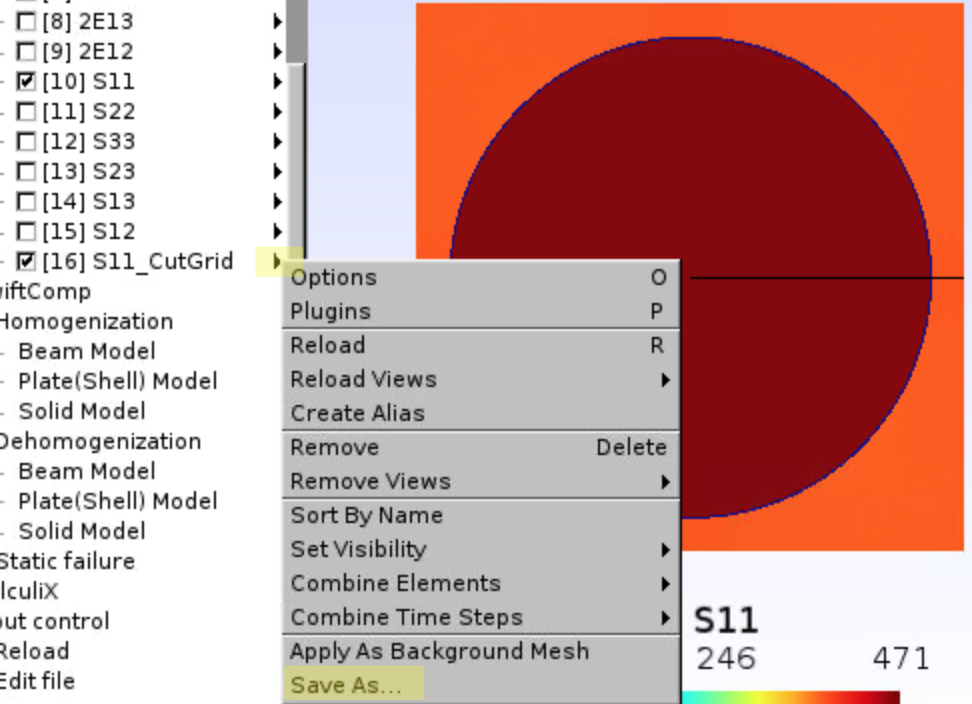
      Fig29_savecut.png
    • File format is selected as Generic TXT(*.txt), since the .txt file will only contain numbers, and is easier to be separated.
      Fig30_txt.png
    • Download the exported CutGrid file to your local computer. Open it in Excel. If you have problems about how to download, please refer to this tutorial – 2.3 Check results and save files.
      Fig31_excelimport.png
    • Find the x values (in the 5th column) and corresponding s11 values (in the 8th column). Plot S11 vs. X.
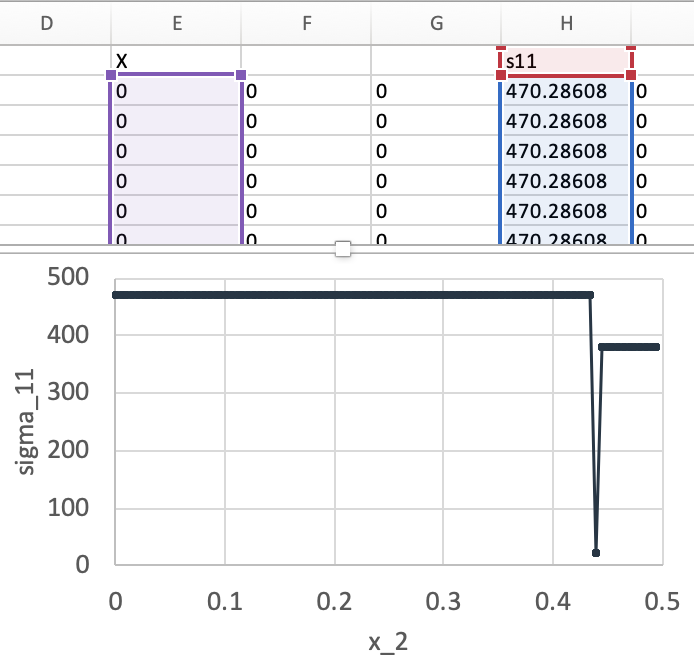
      Fig32_plot.png
    • Since the NumPointsV was set to be 20 by default, there will be 20 points of the same value. Feel free to remove duplicated values in Excel.
    • It’s also good to save as other formats, such as .pos which is the default format. To extract (x,y,z) positions and corresponding S11 values from a .pos file, please refer to this tutorial – Dehomogenization part.

Case 3. 0/90 Laminate

Figure 33 shows the microstructure of a 0/90 laminate.
Fig33_laminate.png
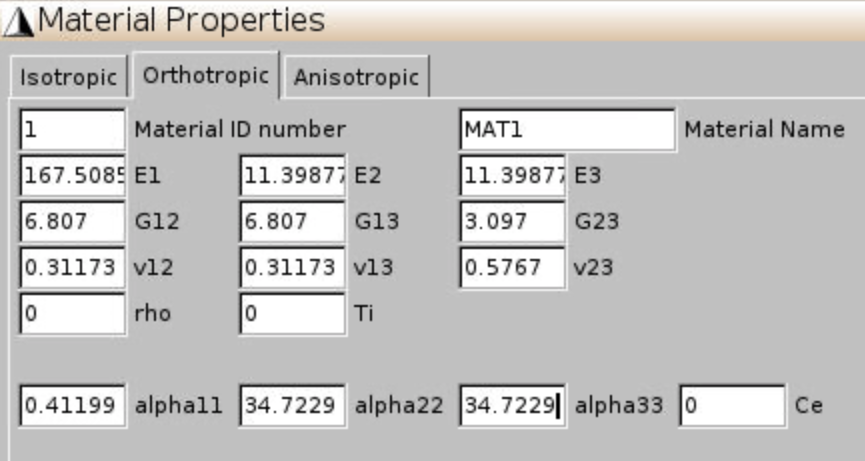
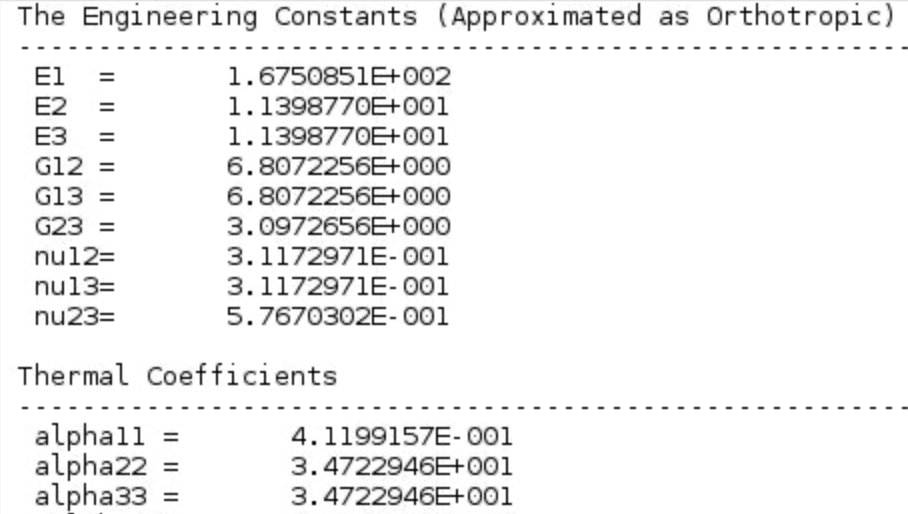
The fiber volume fraction is 60%. Diameter of the fiber is 5 microns. Fiber and matrix properties are the same as given in Figure 2 for Case 1.
We first calculate the effective properties of lamina using square pack geometry, then input lamina properties to calculate the laminate properties.

Solution Procedures

  • Calculate lamina properties
    • Click Material, Thermoelastic, Orthotropic, input matrix and fiber properties given in Figure 2, click Add for each material. Finally click Close.
      (Image(Fig34(1)_Mat1.png, 461px) failed - File not found) (Image(Fig34(2)_Mat2.png, 358px) failed - File not found)
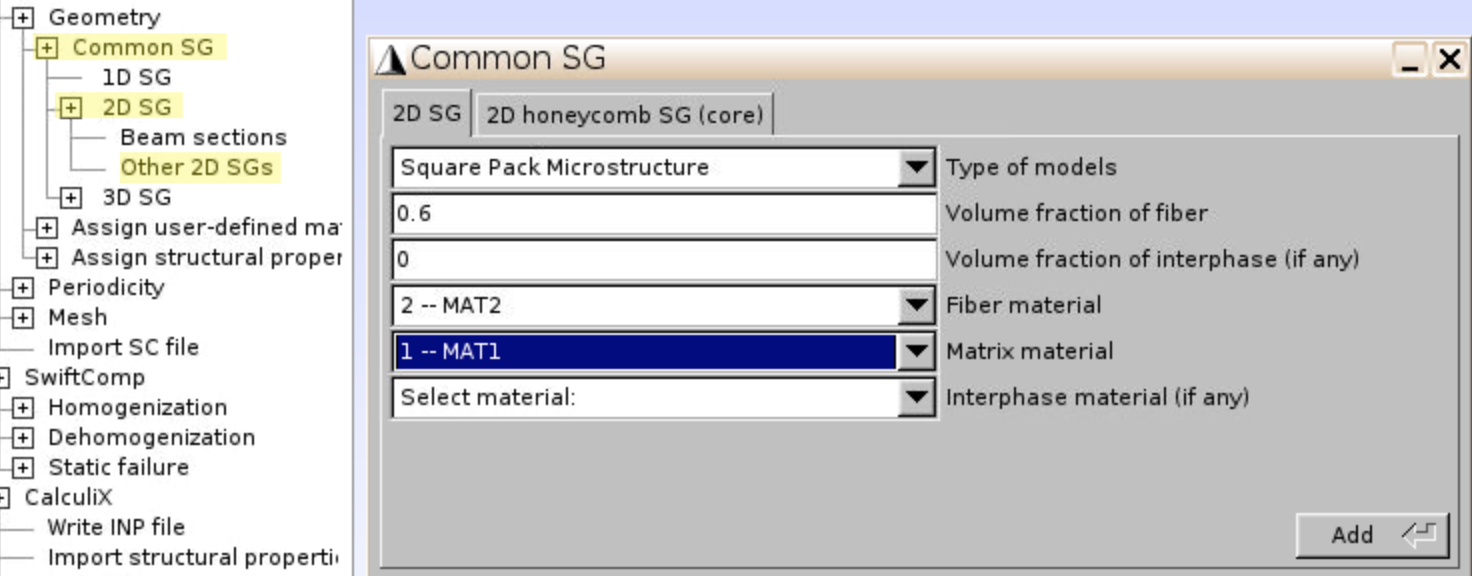
    • Click Geometry, Common SG, 2D SG, Other 2D SGs.
    • Select Type of models: Square Pack Microstructure, input Volume fraction of fiber: 0.6, select Fiber and Matrix materials to be MAT2 and MAT1, click Add.
      Fig35_SquPack.png
    • Click Mesh, Generate 2D mesh, Generate, and Set order 2.
      Fig36_mesh.png
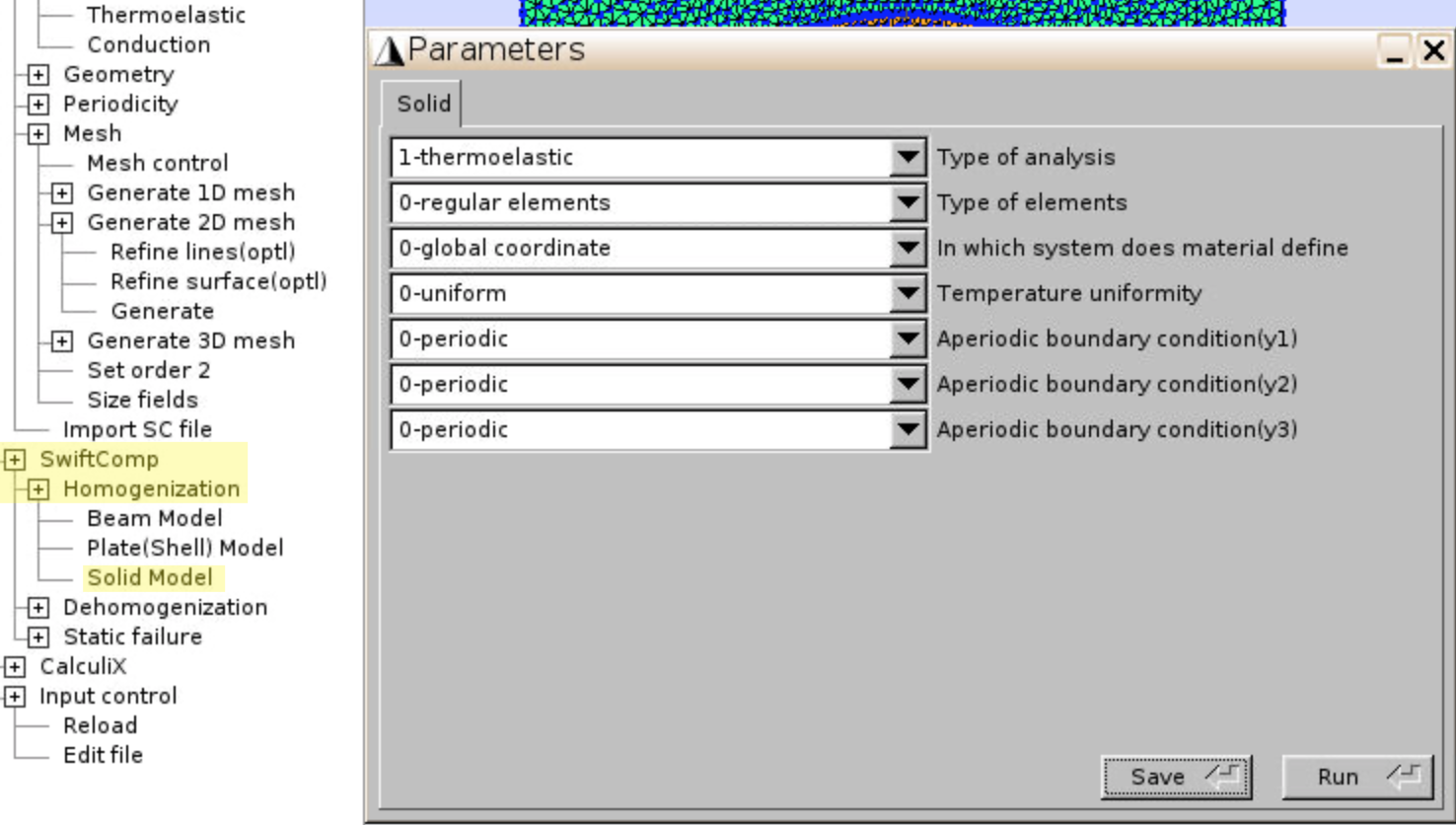
    • Click SwiftComp, Homogenization, Solid Model. Select 1-thermoelastic. Click Save, Run.
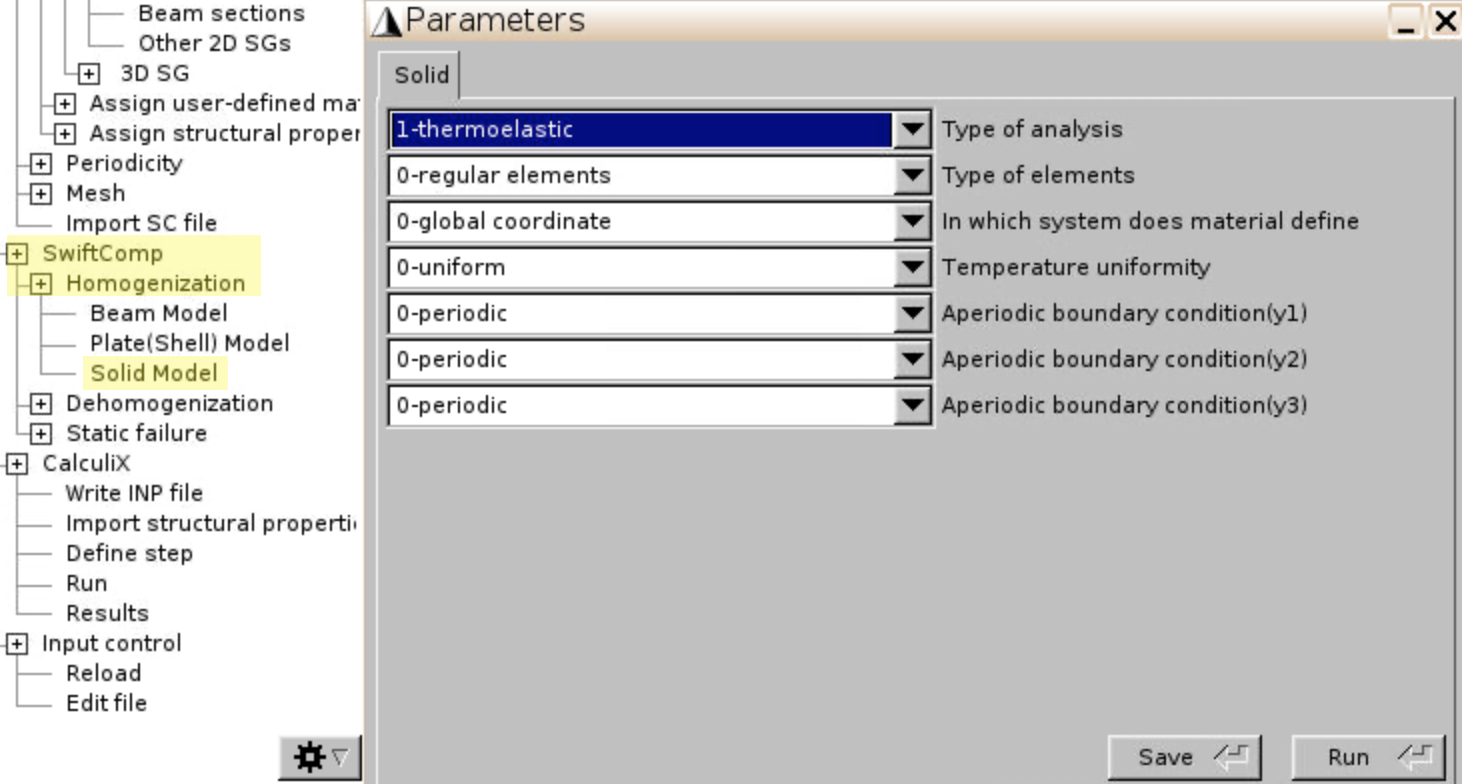
      Fig37_homogenization.png
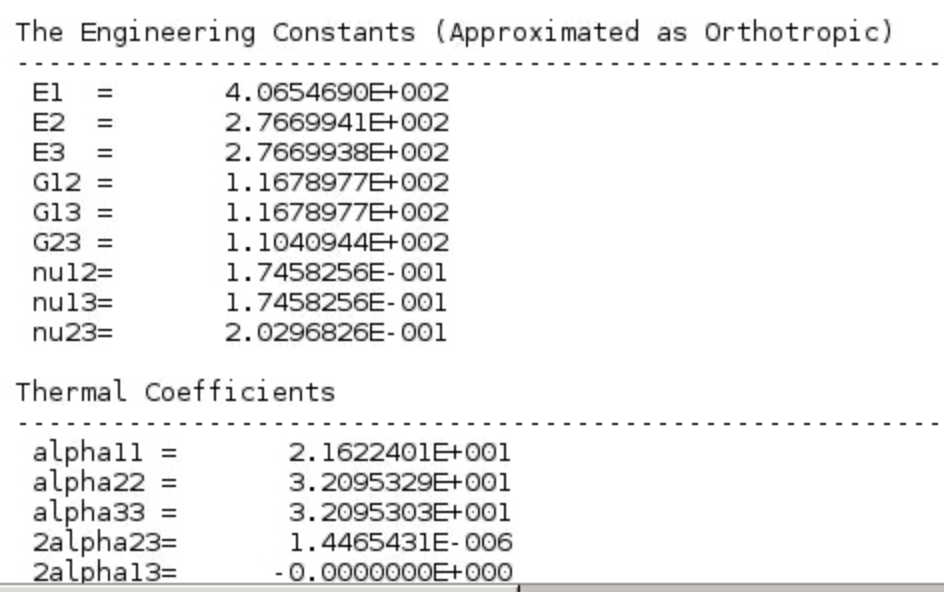
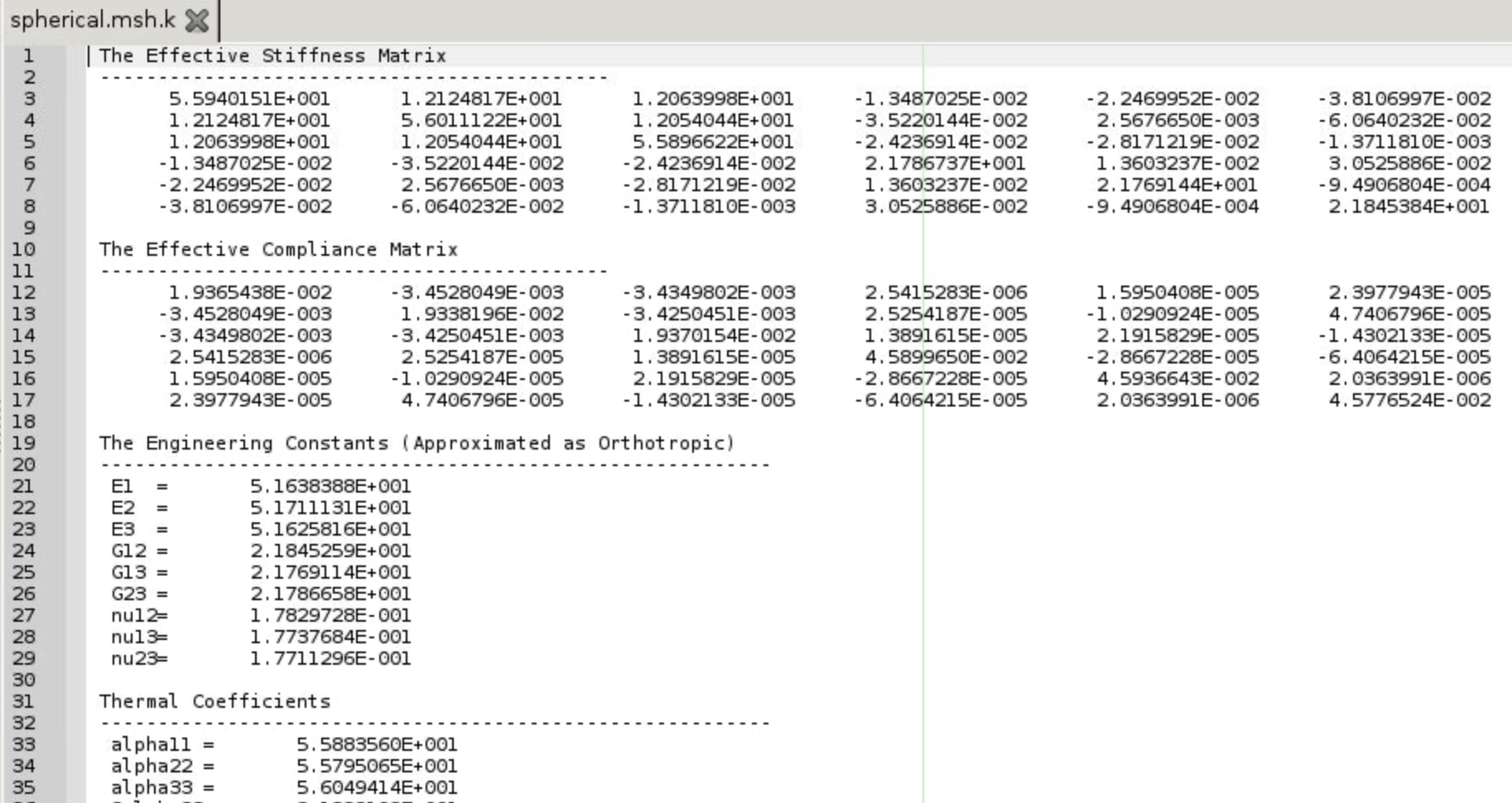
    • Effective lamina properties are given in the .msh.k file.
      Fig38_laminaProp.png
  • Input lamina properties
    • Create a new .geo file for laminate.
      Fig39_new.png
    • Click Material, Thermoelastic, Orthotropic, input lamina properties in Figure 39. Click Add and Close.
      Fig40_LaminaProp.png
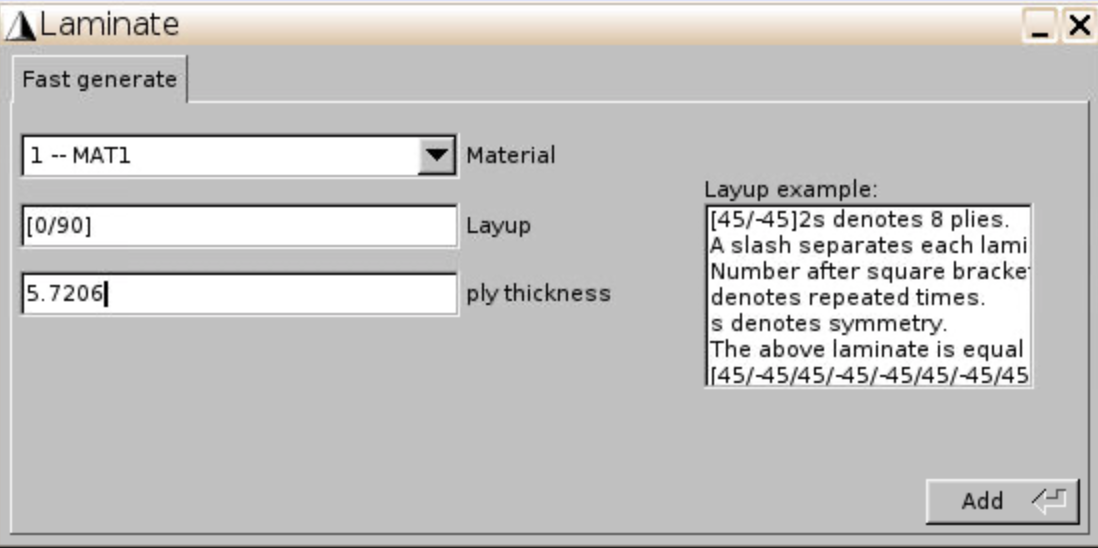
  • Define SG geometry
    • Click Geometry, Common SG, 1D SG, Fast generate.
      Fig41_laminateGen.png
    • Input Layup: [0/90], ply thickness: 5.7206, click Add. The ply thickness is calculated by the fiber volume fraction (0.6) and fiber diameter (5).
      Fig42_thickness.png Fig43_1dSG.png
  • Mesh
    • Click Mesh, Generate 1D mesh, Generate.
  • Homogenization
    • Click SwiftComp, Homogenization, Solid Model. Select 1-thermoelastic. Click Save, Run.
      Fig44_homogenization.png
    • The effective laminate properties are given in msh.k file.
      Fig45_laminateresults.png

Case 4. Double spherical inclusion

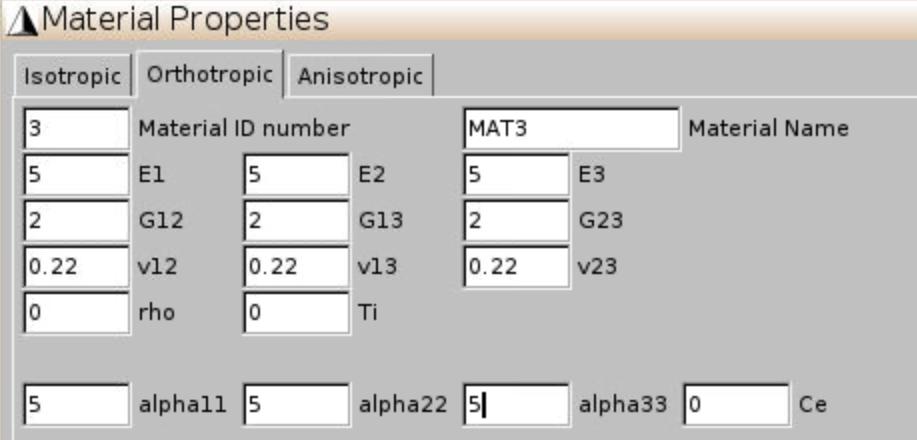
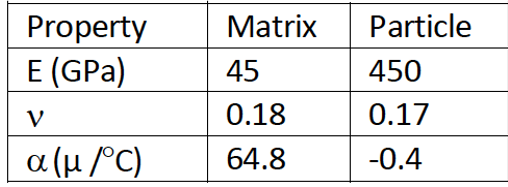
Reinforcing particles or voids in composites are represented by spheres inside a box. The double spherical inclusion microstructure is shown in Figure 46. The box is 2*2*2 microns. Diameter of the two spheres are 1 and 0.5 microns. The larger sphere is centered at (0.6, 0.6, 0.6) and the smaller sphere is centered at (1.5, 1.7, 1.3). Material properties are given in Figure 47.
Fig46_2spheres.png Fig47_properties.png

Solution Procedures

  • Add material properties
    • Click Material, Thermoelastic, input matrix and fiber properties given in Figure 47, click Add for each material. Finally click Close.
      Fig48_Mat1.png Fig49_Mat2.png
  • Define SG geometry
    • SwiftComp already coded the single spherical inclusion microstructure as one of the common SGs. Here we first create one sphere, and edit the commands to create the second sphere.
    • Alternatively, you may download !Gmsh 2.9.3 from http://gmsh.info//bin/, draw the two spheres, and copy the commands into the .geo file on cdmhub.
    • To create an arbitrary spherical inclusion microstructure, click Geometry, Common SG, 3D SG, Other 3D SGs. Select Spherical Inclusions Microstructure, input any number as Volume fraction as we will change the radius later.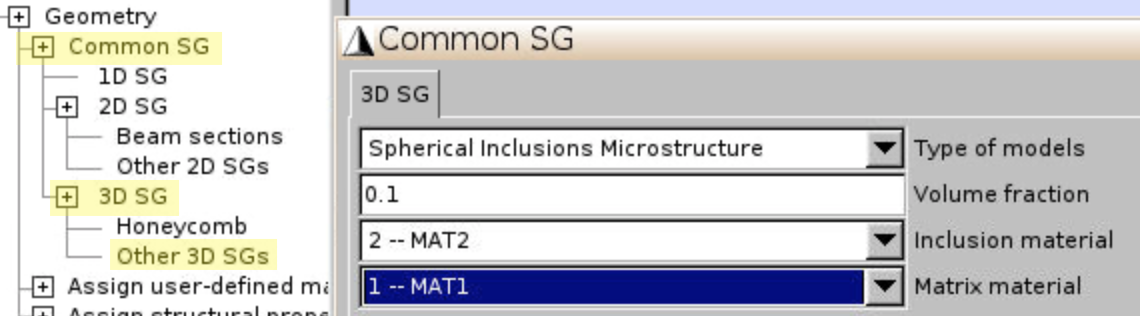
      Fig50_geometry.png
    • Click Input control, Edit file.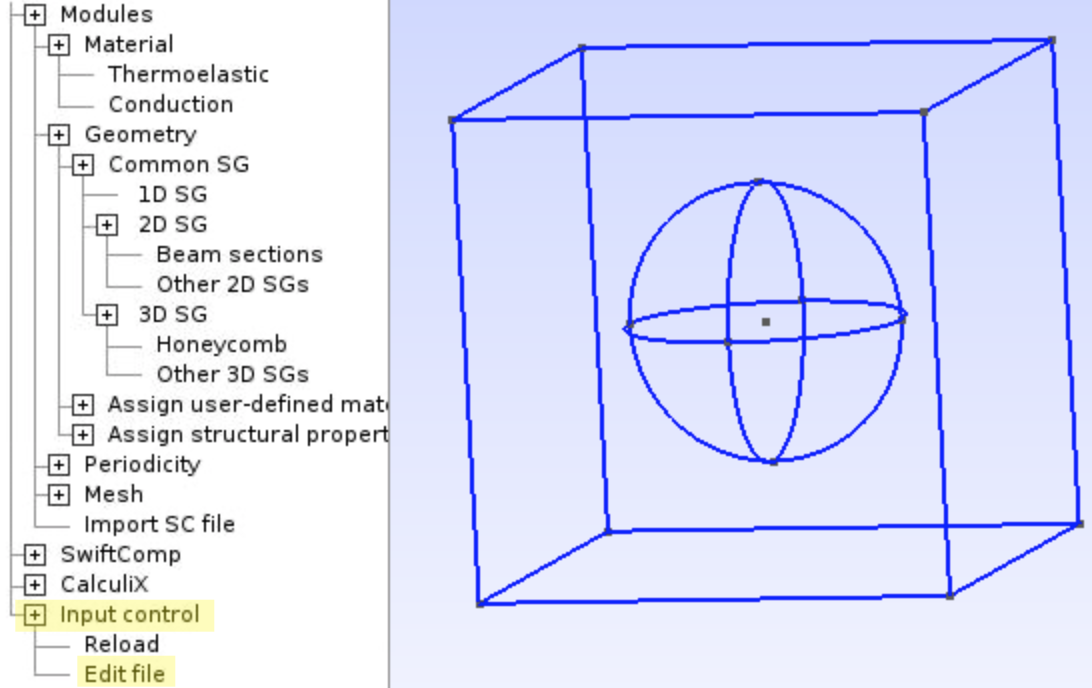
      Fig51_onesphere.png
    • You’ll find the commands that describes the geometry starting from Point (1).
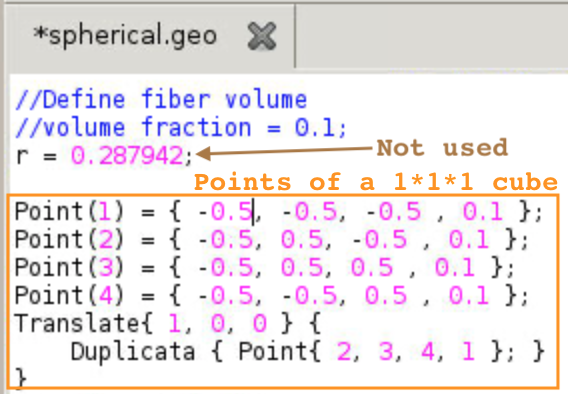
  • Modify the cubic box
    Fig52_editgeo.png (old commands)
    • Points are formatted as Point(#) = {x,y,z, mesh size}.
    • Points (1), (2), (3), (4) define a 1*1 square at x = -0.5, which is the left face of the 1*1*1 cube.
    • Translate of the four points by x+1 to x = 0.5, to get the other four points on the right face of the 1*1*1 cube.
    • The eight points represent a 1*1*1 cube from (-0.5, -0.5, -0.5) to (0.5, 0.5, 0.5)
      Fig53_box.png (new commands)
    • Now change the (x,y,z) numbers so that the cube is 2*2*2, from (0, 0, 0) to (2, 2, 2).
    • Change the mesh size to be 1.
    • Change the Translate distance to be 2.
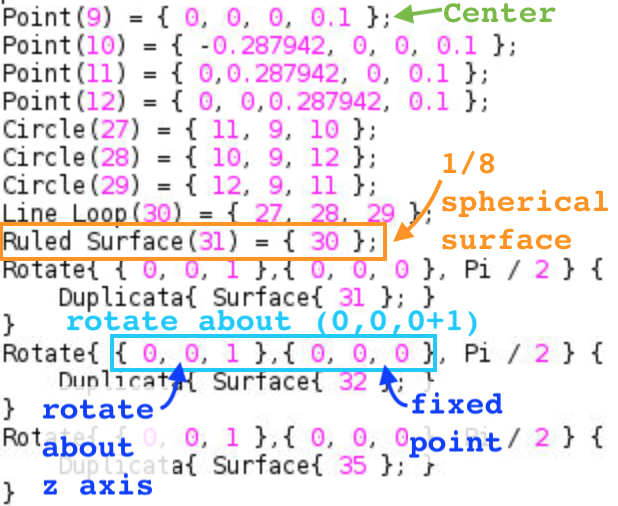
  • Modify the larger sphere
    Fig54_sphere.png (old commands)
    • A 1/8 sphere is defined by 4 points, 3 arcs, and 1 surface. The surface is then rotated 7 times to create the entire sphere.
      Fig55_newpoints.png (new commands)
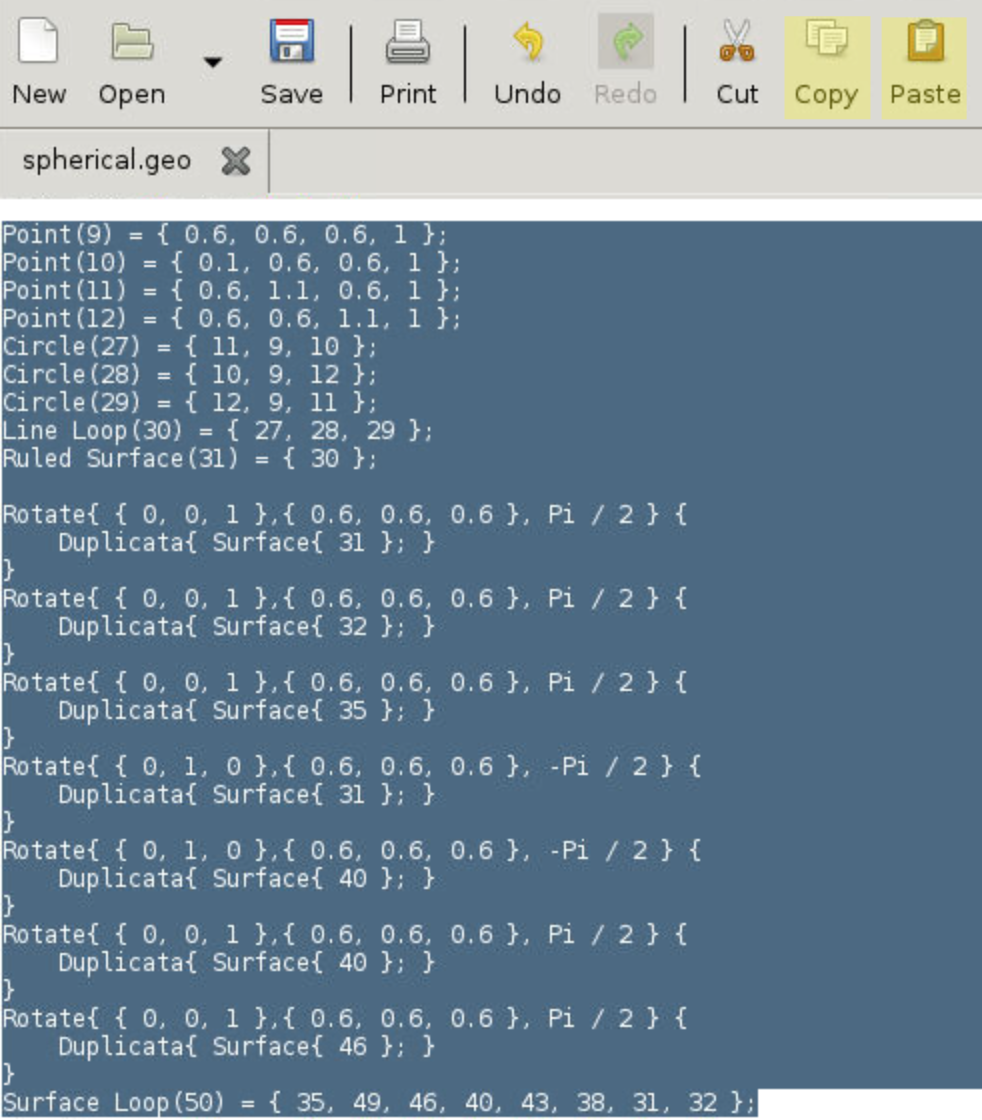
    • Change the (x,y,z) of Point (9) so that the sphere is centered at (0.6, 0.6, 0.6).
    • Points on the surface are (center point +/- radius). The radius of the larger sphere is 0.5.
    • Mesh size is changed to 1 again.
      Fig56_newrotate.png (new commands)
    • Center of rotation should be the spherical center (0.6, 0.6, 0.6).
    • Check the geometry in SwiftComp by clicking Input control, Reload. Feel free to add or remove visible labels in Options.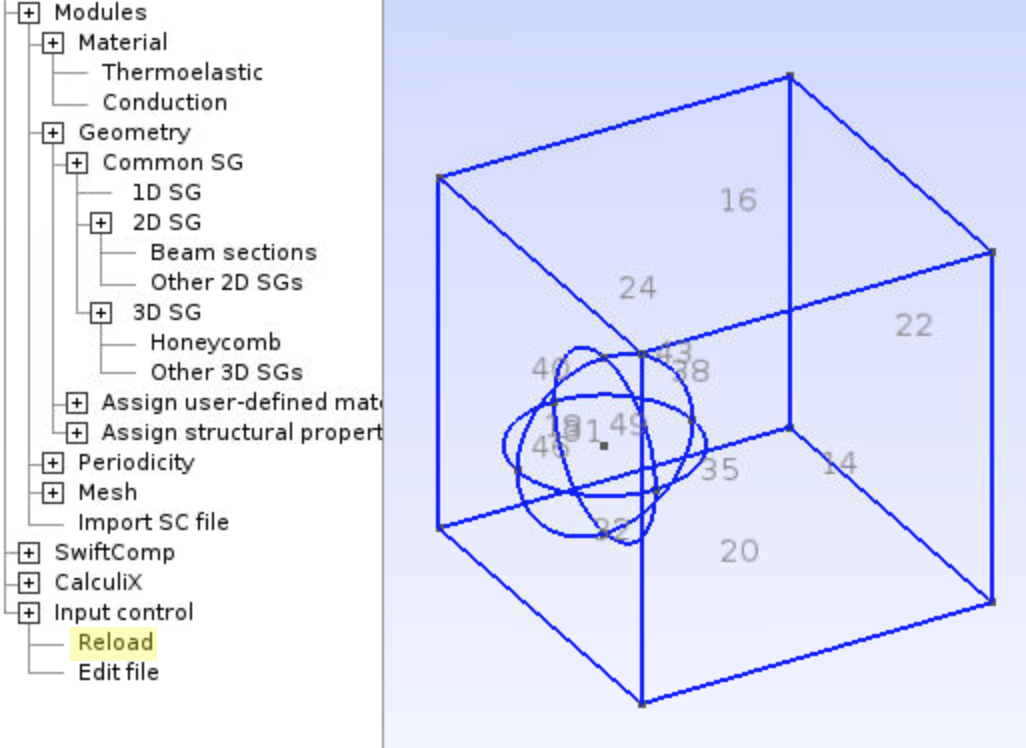
      Fig58_newview.png Fig57_viewsurface.png
  • Create the smaller sphere
    • Select the commands that create the larger sphere, copy and paste.
      Fig59_copysphere.png
    • Change element numbers and (x,y,z) values.
    • To avoid error caused by dummy element number, I did not follow a sequential order, but just changed Point(n) into Point(n+40), and changed Line(m) into Line(m+30). Surfaces are in the same sequence as Lines.
      Fig60_sphere2.png Fig61_sphere2view.png
    • For example, Point(9) is changed into Point(49), Circle(27) is changed into Circle(57). Circle means circle arc which is a line element.
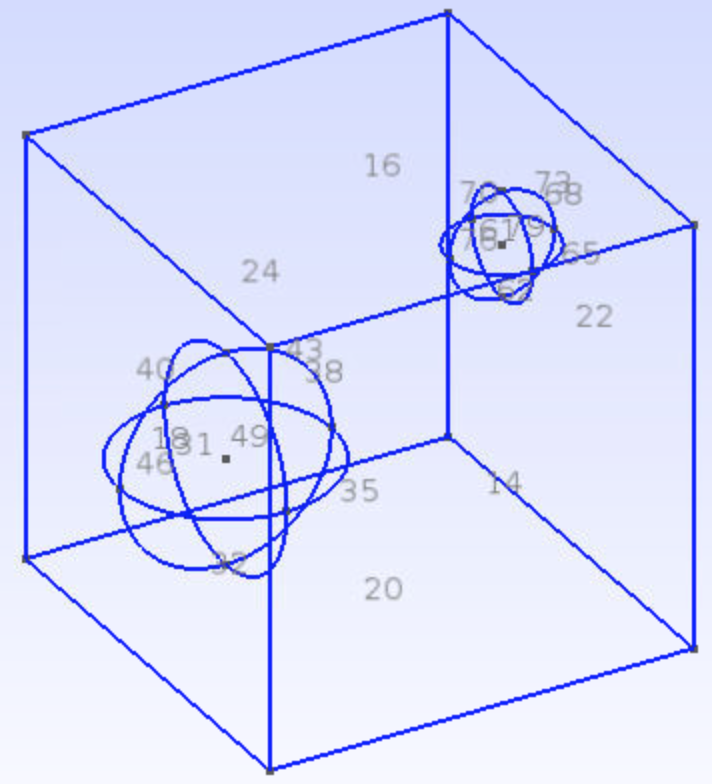
      Fig62_sphere2rotate.png Fig63_allview.png
    • Rotation center should be the spherical center (1.5, 1.7, 1.3). All element numbers in Figure 62 are lines or surfaces, and are changed from m to m+30.
  • Assign material properties
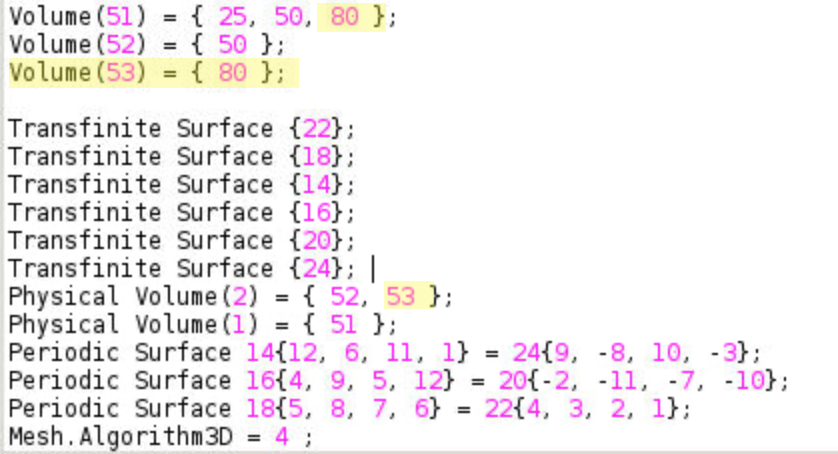
    Fig64_volume.png
    • Volume(51) is the non-particle space (matrix). Volume(51) = {25, 50} means the outer surface is Surface(25) (the cubic box), while the inner hole is Surface(50) (the larger sphere). Add 80 at the end as another inner surface to exclude the small sphere from matrix.
    • Add a new volume for the small sphere.
    • Physical volume (2) is the particle. Add the small sphere. This would assign particle properties to the small sphere.
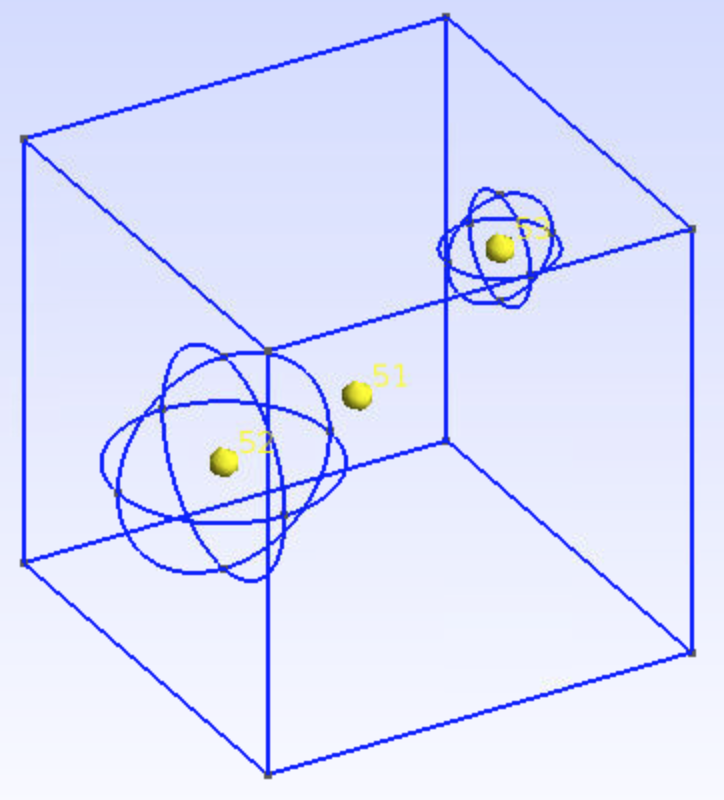
      Fig65_volumeview.png
  • Mesh
    • Click Mesh, Generate 3D mesh, Generate, and Set order 2.
      Fig66_mesh.png
  • Homogenization
    • Click SwiftComp, Homogenization, Solid Model. Select 1-thermoelastic. Click Save, Run.
      Fig67_homogenization.png
    • The effective properties are given in .msh.k file.
      Fig68_results.png

References

  1. Andrew J Ritchey; Hamsasew Sertse; Johnathan Goodsell; Wenbin Yu; Byron Pipes (2015), “Micromechanics Simulation Challenge Level I Results,” https://cdmhub.org/resources/948.
  2. Xin Liu; Wenbin Yu (2017), “Gmsh4SC USER’S MANUAL”, https://cdmhub.org/resources/1342/download/Gmsh4SCManual.pdf

Created on , Last modified on

© 2024 cdmHUB.